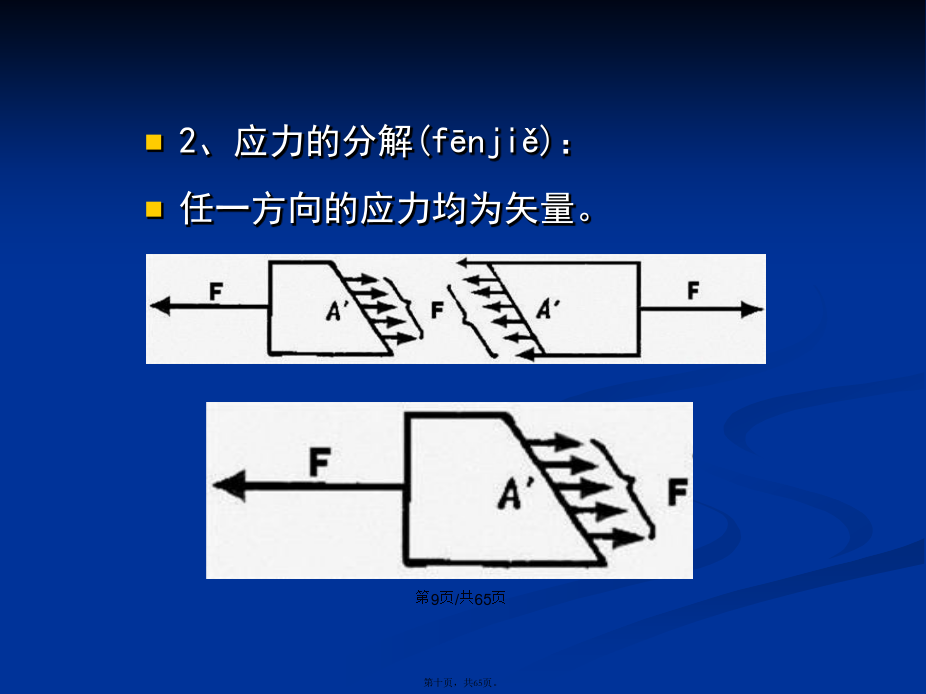
会计学第一节应力(yìnglì)和应变第一节应力和应变物体受到外力作用后，产生两方面(fāngmiàn)效果：一方面(fāngmiàn)产生整体运动;另一方面(fāngmiàn)，外力将向物体内部传递，引起物体内部各相邻点之间相对运动，导致其体积或形状发生改变，使物体产生变形。形变：(deformation)弹性形变：能恢复原状的形变；例如：橡皮筋等。塑性形变：不能或者部分恢复原状的形变；例如：橡皮泥、铜丝(tónɡsī)等。物体的弹性：应力与应变是为研究物体的形变，而引入的两个基本概念。一、应力(stress)应力——是作用于物体内单位面积(miànjī)上的弹性力，它准确地描述了作用于物体内部力的分布情况。应力单位为：N·m-2。图为O点附近的一小(yīxiǎo)元，截面ABC的法线方向为n，当ΔA→0时，点O在n方向的应力为：显然，任一方向的应力均为矢量。我们将应力分解为与作用(zuòyòng)面垂直的分量σ及与作用(zuòyòng)面平行的分量τ。一般称与作用(zuòyòng)面垂直的应力σ为正应力，与作用(zuòyòng)面平行的应力τ为切应力。拉应力(yìnglì)绳的张应力2、应力的分解(fēnjiě)：任一方向的应力均为矢量。将其正交分解为与作用面垂直的分量F⊥，称为(chēnɡwéi)正应力；而与作用面平行的分量F∥，则称为(chēnɡwéi)切应力。切应力(yìnglì)：不同物体(wùtǐ)有不同的正应力（或切应力）阈值。二、应变(strain)物体内部任一小单元，在应力作用下都可发生变形，变形程度用应变来描述。应变——应力作用时，物体的长度、形状或体积发生相应(xiāngyīng)变化(与其原来尺度相比较)。应变是一种无量纲的量。应变有多种形式，按变化(biànhuà)量的不同，应变有：张（线）应变：对一细长物体施加拉力使之拉伸，设物体初始长度为Lo，拉伸后成为（Lo+ΔL），切应变体应变等。则单位长度(chángdù)的伸长率为：称ε为线应变。ΔL为伸长量。若物体被压缩(yāsuō)：ΔL为压缩(yāsuō)量。若物体被压缩(yāsuō)，则ΔL<0，此时有ε<0。切应变(shearstrain)：使长方体下底面固定(gùdìng)，在其上底面平行地加一作用力F，使之形变。切应变——上底面、下底面的相对位移与两底面的垂直距离之比。设上下两底面相对偏移(piānyí)距离为Δx，垂直距离为h，倾斜角为φ，定义切应变γ：泊松比：当物体被纵向(zònɡxiànɡ)拉伸时，横向将收缩。实验表明：横向的相对收缩与纵向(zònɡxiànɡ)相对伸长成正比。对于不可压缩材料为：μ=0.5，而对其他材料则为：μ<0.5。体应变(volumestrain)——物体在各个方向上均受压强P的作用(zuòyòng)，体积变化与原体积之比。第二节弹性模量(tánxìnɡmóliànɡ)一、弹性(tánxìng)与塑性：1、弹性(tánxìng)2、塑性(sùxìng)1、解释(jiěshì)曲线：“a”正比极限；“ab”非比例区；“bc”塑性区；“cd”塑性形变区；“d”断裂点。2、塑性形变——当σ＞σb时，发生(fāshēng)塑性形变。去掉外力后，材料将沿cc’曲线变化，最后留下(liúxià)一段形变oc’。3、强度极限（断裂点）——d点当应力达到d点时，材料发生(fāshēng)断裂。三、弹性模量外力作用(wàilìzuòyònɡ)使物体形变，力与形变之间关系，可用应力与应变之间函数关系表示。1、弹性模量——材料应力与应变的比值。在正比极限内，应力与应变成正比。不同材料其比值也不同。弹性模量的单位：Pa=N/m22、公式杨氏模量——物体(wùtǐ)受张应力或压应力作用时，其应力与应变的比值。各种(ɡèzhǒnɡ)固体的杨氏模量数值表切变模量——切应力与切应变的比值(bǐzhí)。大多数金属的体切变模量为：（E/3～E/2）。各种(ɡèzhǒnɡ)固体的切变模量数值表体变模量（K）——压强与体应变的负比值(bǐzhí)。体积压缩系数（k）——体变模量的倒数。各种固、液体(yètǐ)的体变模量数值表3、例题(lìtí)已知：骨长Lo=0.4m，S=5Cm2，F=500N，E=1×1010N/m2。求：ΔL=？（ΔL/Lo）=？/4、应力(yìnglì)、应变、弹性模量公式小结一览表应力(yìnglì)分类应力(yìnglì)应变模量（名称)张、压应力(yìnglì)切应力(yìnglì)体压强三、弹性模量在正比极限范围内，应力(yìnglì)与应变的变化关系是线性的，它们