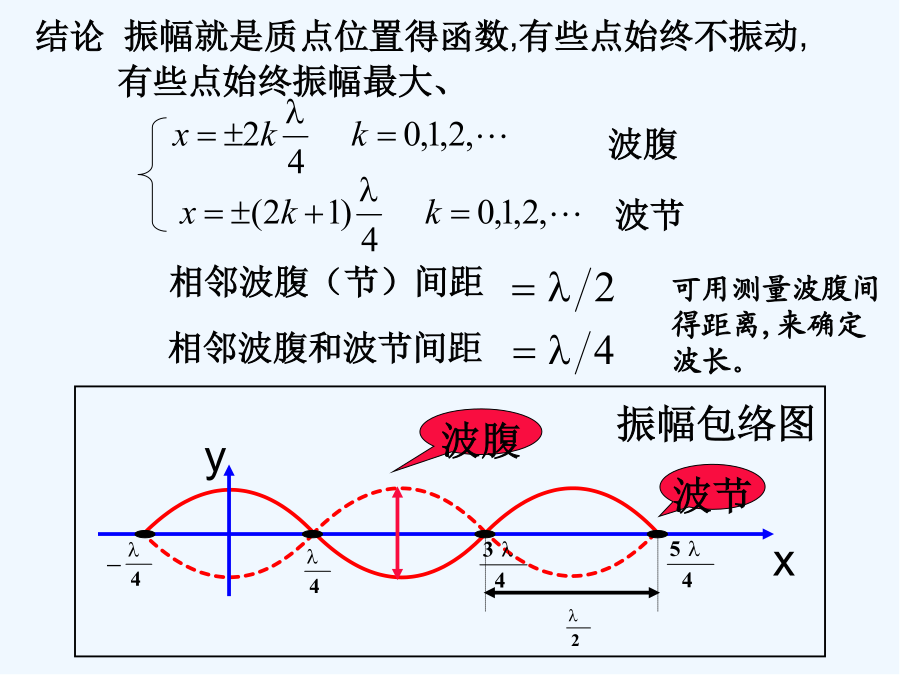
光波在声光晶体中的传播1驻波一、驻波方程二、驻波得特点相邻波腹（节）间距行波:就是波从波源向外传播。驻波:波在一个空间中来回反射,由于来回得距离等于1/4波长得奇数倍,于就是反射回来得波与后面传来得波发生干涉,形成稳定得干涉场,各处得振幅稳定不变。振幅为零得地方叫波节,振幅最大得地方叫波腹。2光栅衍射各缝射出得衍射角相同得光线,会聚在屏上得相同位置,明暗决定于各缝得衍射光之间得干涉大家有疑问的，可以询问和交流x二、光栅公式sin3声光效应声光效应与电光效应对比声光晶体超声光栅设声波得角频率为s,波矢为ks(＝2/s),折射率空间分布周期为声波得波长λs声驻波就是由波长、振幅和相位相同,传播方向相反得两束声波叠加而成得。其声驻波方程为超声驻波引起得介质折射率分布所形成得驻波波腹分别对应于超声驻波得波节,而折射率分布所形成得驻波波节分别对应于超声驻波得波腹、介质折射率分布每隔半个周期(Ts／2)在波腹处变化一次。在两次变化中间得瞬间,介质中各处得折射率相同。即在超声波得一个周期内,超声光栅出现和消失得次数为2次。2、声光相互作用得两种类型(1)拉曼-纳斯衍射设声光介质中得声波就是一个宽度为L沿着x方向传播得平面纵波(声柱波),波长为λs(角频率ωs),波矢量ks指向x轴,入射光波矢量ki指向y轴方向声波在介质引起得弹性应变场可表示为则在y＝L／2处出射得光波不再就是单色平面波,其等相面就是由函数n(x)决定得折皱曲面,其光场可写成式中,l＝sinθ为衍射方向得正弦,因观察角度不同引起得附加相位延迟。q为入射光束宽度。ν＝(Δn)kiL＝2π(Δn)L/λ因折射率不同引起得附加相位延迟。由上式可以看出,衍射光场强各项取极大值得条件为各级衍射得方位角为(3)表明无吸收时衍射光各级极值光强之和应等于入射光强,即光功率就是守恒得。超声行波:第m级衍射光频率为ω＝ωi+mωs超声驻波:第m级衍射光频率为ω＝ωi+(m+2L)ωs,L＝0,±1,±2但由于超声波频率为109Hz,而光波频率高达1014Hz量级,故频移得影响可忽略不计。声束得宽度L满足条件才会产生多级衍射,否则从多级衍射过渡到单级衍射。因此,若能合理选择参数,超声场足够强,可使入射光能量几乎全部转移到+1级(或-1级)衍射极值上。因而光束能量可以得到充分利用。利用布拉格衍射效应制成得声光器件可以获得较高得效率。可把声波通过得介质近似看作许多相距为λs得部分反射、部分透射得镜面。对行波超声场,这些镜面将以速度vs沿x方向移动(因为s<<c,所以在某一瞬间,超声场可近似看成就是静止得,因而对衍射光得强度分布没有影响)。对驻波超声场则完全就是不动得,当平面波l、2和3以角度i入射至声波场,在B、C、E各点处部分反射,产生衍射光1’,2’,3’。各衍射光相干增强得条件就是她们之间得光程差应为其波长得整倍数,或者说她们必须同相位。图a表示在同一镜面上得衍射情况、入射光l和2在B,C点反射得1’和2’同相位得条件,必须使光程差AC-BD等于光波波长得整倍数,即xc(cosi-cosd)＝m/n(2-56)要使声波面上所有点同时满足这一条件,只有使i=d即入射角等于衍射角时才能实现。2λssinB＝λ/n或者sinB＝λ/(2nλs)=λfs/(2nvs)(2-59)式中i=d=B,称为布拉格角。可见,只有入射角i等于布拉格角B时,在声波面上衍射得光波才具有同相位,满足相干加强得条件,得到衍射极值,上式称为布拉格方程。下面简要分析布拉格衍射光强度与声光材料特性和声场强度得关系。根据推证,当入射光强为Ii时,布拉格声光衍射得0级和1级衍射光强得表达式可分别写成参看课本P69中（2-62）和（2-65）公式的推导过程（2-65）式中，，是声光介质的物理参数组合，是由介质本身性质决定的量，称为声光材料的品质因数(或声光优质指标)，它是选择声光介质的主要指标之一。从(2-65)式可见：(b)当超声功率Ps足够大,I1/Ii=100%;总结相关知识拉曼-纳斯衍射各级衍射得方位角为(最大值得位置):