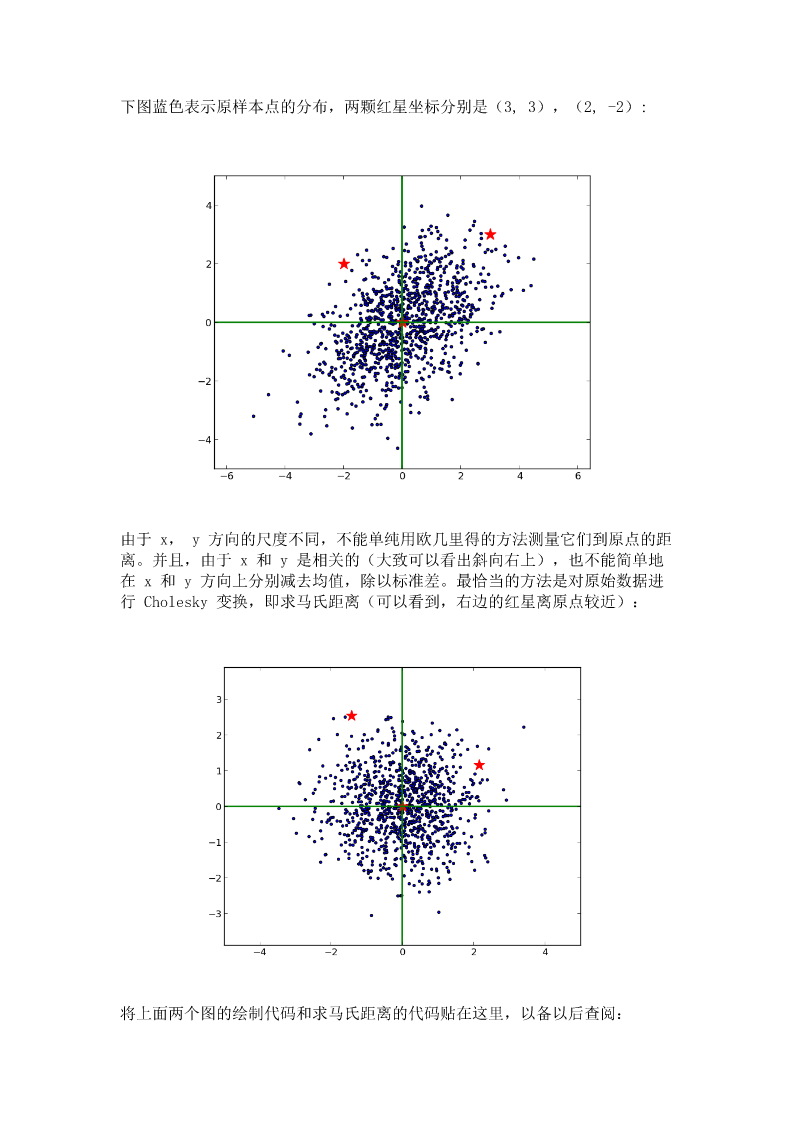
在机器学习和数据挖掘中，我们经常需要知道个体间差异的大小，进而评价个体的相似性和类别。最常见的是数据分析中的相关分析，数据挖掘中的分类和聚类算法，如K最近邻（KNN）和K均值（K-Means）等等。根据数据特性的不同，可以采用不同的度量方法。一般而言，定义一个距离函数d(x,y),需要满足下面几个准则：1)d(x,x)=0//到自己的距离为02)d(x,y)>=0//距离非负3)d(x,y)=d(y,x)//对称性:如果A到B距离是a，那么B到A的距离也应该是a4)d(x,k)+d(k,y)>=d(x,y)//三角形法则:(两边之和大于第三边)这篇博客主要介绍机器学习和数据挖掘中一些常见的距离公式，包括：1.闵可夫斯基距离2.欧几里得距离3.曼哈顿距离4.切比雪夫距离5.马氏距离6.余弦相似度7.皮尔逊相关系数8.汉明距离9.杰卡德相似系数10.编辑距离11.DTW距离12.KL散度1.闵可夫斯基距离闵可夫斯基距离（Minkowskidistance）是衡量数值点之间距离的一种非常常见的方法，假设数值点P和Q坐标如下：那么，闵可夫斯基距离定义为：该距离最常用的p是2和1,前者是欧几里得距离（Euclideandistance），后者是曼哈顿距离（Manhattandistance）。假设在曼哈顿街区乘坐出租车从P点到Q点，白色表示高楼大厦，灰色表示街道：绿色的斜线表示欧几里得距离，在现实中是不可能的。其他三条折线表示了曼哈顿距离，这三条折线的长度是相等的。当p趋近于无穷大时，闵可夫斯基距离转化成切比雪夫距离（Chebyshevdistance）：我们知道平面上到原点欧几里得距离（p=2）为1的点所组成的形状是一个圆，当p取其他数值的时候呢？注意，当p<1时，闵可夫斯基距离不再符合三角形法则，举个例子：当p<1,(0,0)到(1,1)的距离等于(1+1)^{1/p}>2,而(0,1)到这两个点的距离都是1。闵可夫斯基距离比较直观，但是它与数据的分布无关，具有一定的局限性，如果x方向的幅值远远大于y方向的值，这个距离公式就会过度放大x维度的作用。所以，在计算距离之前，我们可能还需要对数据进行z-transform处理，即减去均值，除以标准差：:该维度上的均值:该维度上的标准差可以看到，上述处理开始体现数据的统计特性了。这种方法在假设数据各个维度不相关的情况下利用数据分布的特性计算出不同的距离。如果维度相互之间数据相关（例如：身高较高的信息很有可能会带来体重较重的信息，因为两者是有关联的），这时候就要用到马氏距离（Mahalanobisdistance）了。2.马氏距离考虑下面这张图，椭圆表示等高线，从欧几里得的距离来算，绿黑距离大于红黑距离，但是从马氏距离，结果恰好相反：马氏距离实际上是利用Choleskytransformation来消除不同维度之间的相关性和尺度不同的性质。假设样本点（列向量）之间的协方差对称矩阵是，通过CholeskyDecomposition（实际上是对称矩阵LU分解的一种特殊形式，可参考之前的博客）可以转化为下三角矩阵和上三角矩阵的乘积：。消除不同维度之间的相关性和尺度不同，只需要对样本点x做如下处理：。处理之后的欧几里得距离就是原样本的马氏距离：为了书写方便，这里求马氏距离的平方）：下图蓝色表示原样本点的分布，两颗红星坐标分别是（3,3），（2,-2）:由于x，y方向的尺度不同，不能单纯用欧几里得的方法测量它们到原点的距离。并且，由于x和y是相关的（大致可以看出斜向右上），也不能简单地在x和y方向上分别减去均值，除以标准差。最恰当的方法是对原始数据进行Cholesky变换，即求马氏距离（可以看到，右边的红星离原点较近）：将上面两个图的绘制代码和求马氏距离的代码贴在这里，以备以后查阅：ViewCode马氏距离的变换和PCA分解的白化处理颇有异曲同工之妙，不同之处在于：就二维来看，PCA是将数据主成分旋转到x轴（正交矩阵的酉变换），再在尺度上缩放（对角矩阵），实现尺度相同。而马氏距离的L逆矩阵是一个下三角，总体来说是一个仿射变换。3.向量内积向量内积是线性代数里最为常见的计算，实际上它还是一种有效并且直观的相似性测量手段。向量内积的定义如下：直观的解释是：如果x高的地方y也比较高，x低的地方y也比较低，那么整体的内积是偏大的，也就是说x和y是相似的。举个例子，在一段长的序列信号A中寻找哪一段与短序列信号a最匹配，只需要将a从A信号开头逐个向后平移，每次平移做一次内积，内积最大的