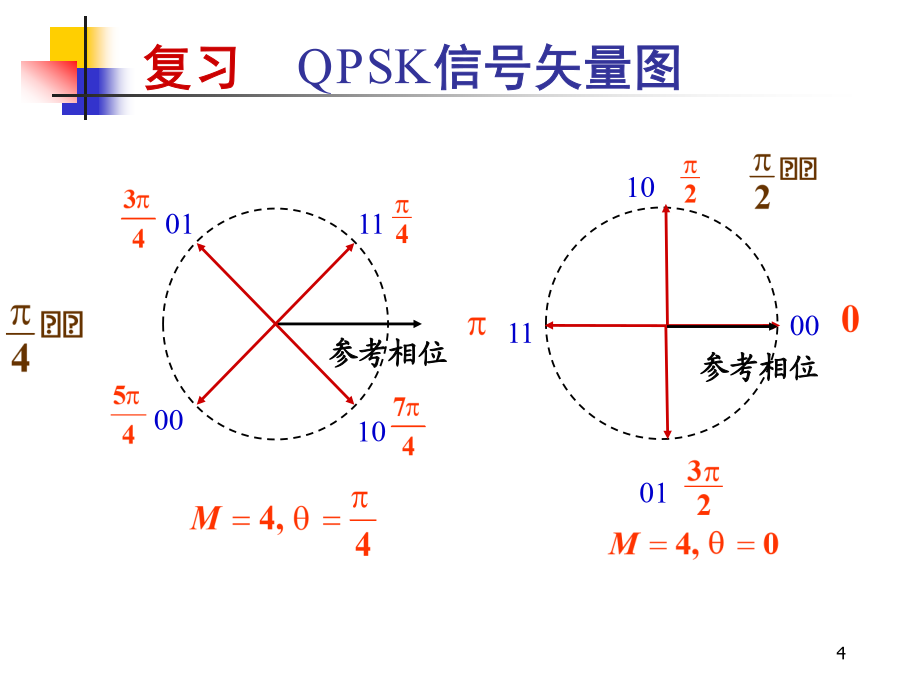
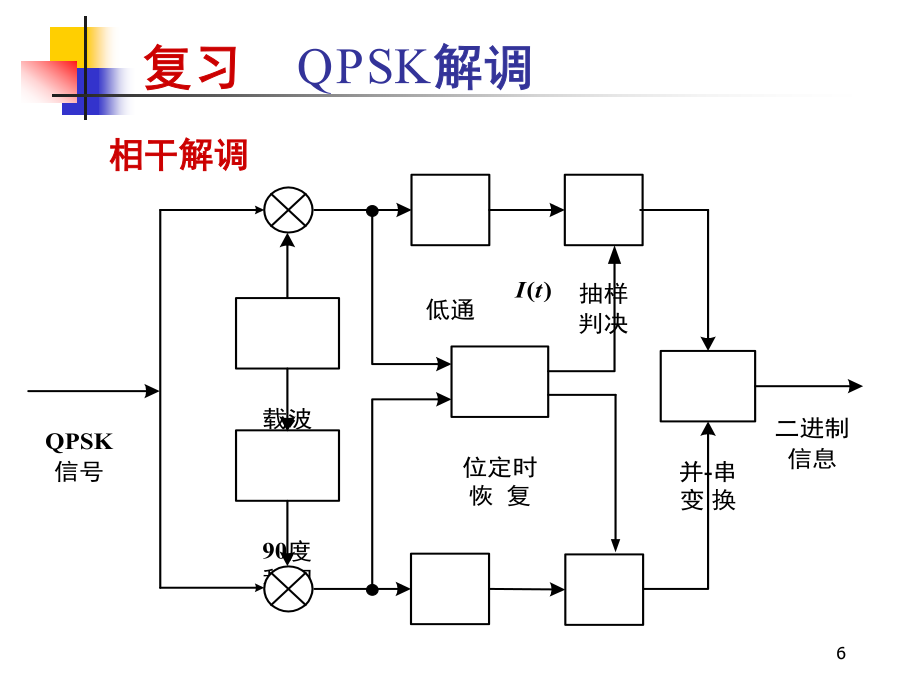
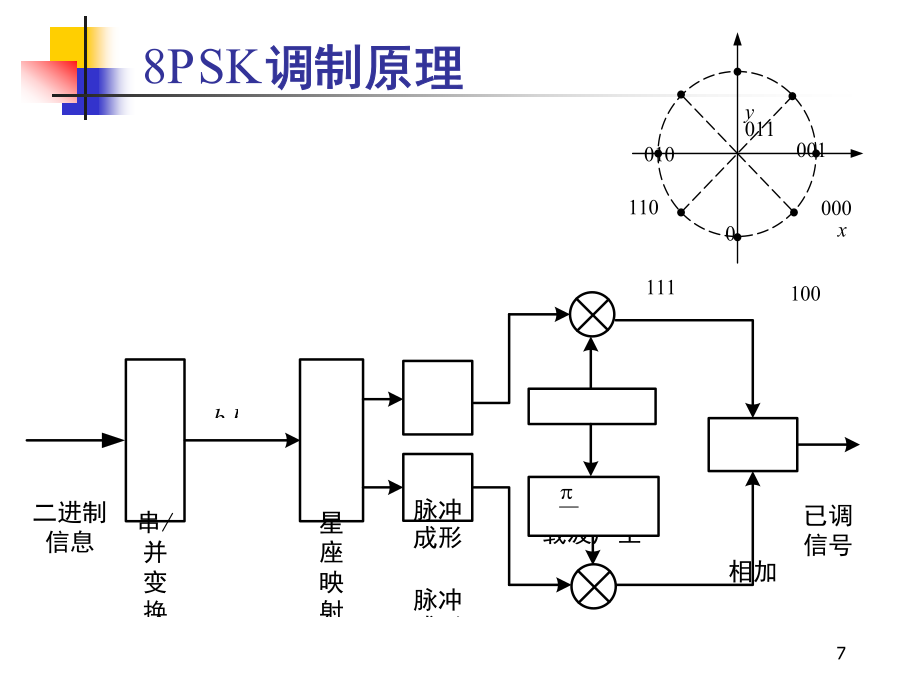
通信原理复习--Eb/n0与S/N复习--MPSK信号表示复习--QPSK信号矢量图复习--QPSK调制复习--QPSK解调8PSK调制原理一种8PSK星座影射关系5.4多进制数字调制原理5.4多进制数字调制原理5.4多进制数字调制原理5.4多进制数字调制原理5.4多进制数字调制原理5.4多进制数字调制原理5.4多进制数字调制原理5.4多进制数字调制原理5.4多进制数字调制原理5.4多进制数字调制原理第7章数字频带传输系统5.5多进制数字调制系统的抗噪声性能抑制载波MASK信号的表示式：若接收端的解调前信号无失真，仅附加有窄带高斯噪声，忽略常数衰减因子后解调前的接收信号为设接收机采用相干解调，则噪声中只有和信号同相的分量有影响。信号和噪声在相干解调器中与载波相乘，并滤除高频分量之后，得到解调器输出电压为对解调器输出电压进行抽样判决。对于抑制载波MASK信号，判决电平应该选择在0、2d、…、(M-2)d。当噪声抽样值|nc|超过d时，会发生错误判决。对于信号电平等于(M-1)d的情况。当信号电平等于+(M-1)d时，若nc>+d，不会发生错判；当信号电平等于-(M-1)d时，若nc<-d，也不会发生错判。当抑制载波MASK信号以等概率发送时，即每个电平的发送概率等于1/M时，平均误码率等于P(|nc|>d)－噪声抽样绝对值大于d的概率。nc是均值为0，方差为n2的正态随机变量，故有5.5多进制数字调制系统的抗噪声性能误码率和信噪比的关系对于等概率的抑制载波MASK信号，其平均功率等于当M=2时，上式变为误码率曲线5.5.2MFSK系统的抗噪声性能1、非相干解调时的误码率分析模型误码率分析计算A.假设：a.当某个码元输入时，M个带通滤波器的输出中仅有一个是信号加噪声，其它各路都只有噪声。b.M路带通滤波器中的噪声是互相独立的窄带高斯噪声，其包络服从瑞利分布。故这(M-1)路噪声的包络都不超过某个门限电平h的概率等于P(h)是一路滤波器的输出噪声包络超过门限h的概率，由瑞利分布公式，等于任意一路或一路以上噪声输出的包络超过此门限就将发生错误判决，错判的概率将等于和门限值h有关。有信号码元输出的带通滤波器的输出电压包络服从广义瑞利分布：其它路中任何路的输出电压值超过了有信号这路的输出电压值x就将发生错判。输出信号和噪声之和x就是门限值h。发生错误判决的概率是由于一个M进制码元含有k比特信息，所以每比特占有的能量等于E/k，比特信噪比：若用M代替(M-1)/2，不等式右端的值将增大，但是此不等式仍然成立，有当k时，Pe按指数规律趋近于0，但要保证只要保证比特信噪比rb大于2ln2=1.39＝1.42dB，则不断增大k，就能得到任意小的误码率。误码率Pe和误比特率Pb之间的关系假定当一个M进制码元发生错误时，将随机地错成其它(M-1)个码元之一。由于M进制信号共有M种不同的码元，每个码元中含有k个比特，M=2k。在一个码元中的任一给定比特的位置上，出现“1”和“0”的码元各占一半，即出现信息“1”的码元有M/2种，出现信息“0”的码元有M/2种。实例：M=8，k=3，在任一列中均有4个“0”和4个“1”。若一个码元错成另一个码元时，在给定的比特位置上发生错误的概率只有4/7。在一个给定的码元中，任一比特位置上的信息和其它(2k-1–1)种码元在同一位置上的信息相同，和其它2k-1种码元在同一位置上的信息不同。误比特率Pb和误码率Pe之间的关系为误码率曲线2、相干解调时的误码率计算结果：A.误码率上界：B.误码率曲线C.比较相干和非相干解调的误码率：当k>7时，两者的区别可以忽略。5.5.3MPSK系统的抗噪声性能QPSK系统的性能A.噪声容限B.误码率：设f()为接收矢量（包括信号和噪声）相位的概率密度，则错误概率为C.信号表示式D.当QPSK码元的相位k等于45时，E.信号码元相当于是互相正交的两个2PSK码元，其功率为接收信号功率的(1/2)倍。接收信号与噪声之和为F.若把此QPSK信号当作两个2PSK信号分别进行相干解调时，只有和2PSK信号同相的噪声才有影响。G.根据2PSK相干解调的误码率得到：I.只有两路正交的相干检测都正确，才能保证QPSK信号的解调输出正确。两路正交相干检测都正确的概率为J.QPSK信号解调错误的概率为对于任意M进制PSK信号，误码率为A.当M大时，MPSK误码率公式可以近似为B.OQPSK的抗噪声性能和QPSK完全一样。C.对于M相绝对移相方式，当信噪比r足够大时，误码率可近似为5