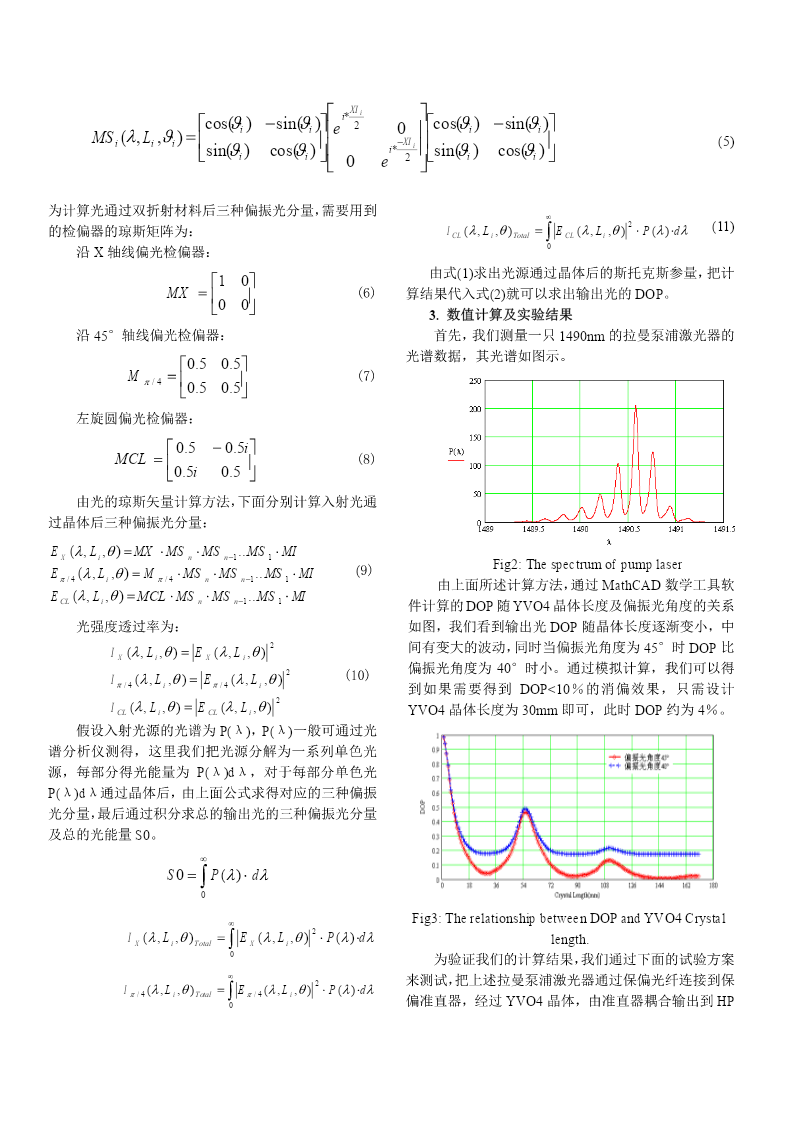
一种基于Jones矩阵的偏振度计算方法研究罗勇(武汉光迅科技有限责任公司，湖北武汉430074)摘要：本文提出了一种采用琼斯矩阵直接分析光源通过双折射材料后的斯托克斯参量，进而分析其偏振度（DOP）的数值计算方法。本方法的优点在于可以计算任意光谱的光源通过双折射材料后的DOP，本文对一个拉曼泵浦激光光源通过YVO4晶体后的DOP与晶体长度的关系进行了理论计算，并与实际测试结果进行了比较，两者结果是一致的。关键词：琼斯矩阵；斯托克斯参量；拉曼泵浦；退偏器1.引言S3），S0为总的光强度，S1＝Ix-Iy，Ix为延X轴偏振光强在分析双折射材料对光源偏振度（DOP）的影响时，度分量，Iy为延Y轴偏振光强度分量，S2＝Iπ/4-I-π/4，Iπ一般采用光波的相干矩阵和双折射材料的琼斯矩阵来/4为沿+π/4方向的线偏振光强度分量，I-π/4为沿-π/4计算输出光的偏振度，在分析过程中往往是把光源光方向的线偏振光强度分量，S3＝ICL-ICR，ICL为左旋圆偏谱等效为矩形光谱或高斯型光谱来简化计算。本文提振光强度分量，ICR为右旋圆偏振光强度分量，同时S0出了一种采用琼斯矩阵和斯托克斯参量分析偏振度＝ICL+ICR＝Iπ/4+I-π/4＝Ix+Iy，为了计算方便一般把上面（DOP）的方法，可以对任意谱形的光源设计消偏所公式化为如下表达［2］：需的双折射晶体或保偏光纤的长度。实际应用中只需⎧SIS1=2x−0测试光源光谱，就可以使用本文说明的方法模拟光源⎪⎨SIS2=2π4/−0（1）通过双折射材料（如双折射光纤、晶体等）后的偏振⎪度，可用来设计各种基于双折射材料的退偏器。文中⎩SIS3=2CL−0实际分析了一个拉曼泵源激光光源DOP随YVO4晶因此，实际计算中我们只需要计算三种偏振光强度分体长度和晶体光轴变化的关系，并与试验测试结果进量：延X轴偏振光强度分量、沿+π/4方向的线偏振光行了比较分析。强度分量及左旋圆偏振光强度分量。2.理论分析斯托克斯参量与偏振度（DOP）的关系如下：SSS12+22+32DOP=（2）S0λ输入线偏光的琼斯矩阵：X⎡cos(β)⎤MI()β=⎢⎥（3）β⎣sin(β)⎦θi其中β为偏振方向与x轴夹角。晶体的相位延迟：LiY2π⋅Δn(λ)⋅LXI()λ=i（4）iλFig1:Theorymodeofopticsourceandbirefringencecrystal其中△n为晶体的双折射，d为晶体长度，λ为光如图偏振光源与X轴夹角为θ,双折射晶体或光纤波长。其琼斯矩阵为：长度为Li,光轴与X轴夹角为θi。这里我们采用通过Jones矩阵计算出输出光的斯托克斯参量（S0，S1，S2，XI⎡i*i⎤cos(ϑ)−sin(ϑ)2cos(ϑ)−sin(ϑ)⎡ii⎤⎢e0⎥⎡ii⎤MSi(,,)λLiϑi=−XI(5)⎢⎥⎢i*i⎥⎢⎥⎣sin(ϑi)cos(ϑi)⎦2⎣sin(ϑi)cos(ϑi)⎦⎣0e⎦为计算光通过双折射材料后三种偏振光分量，需要用到∞IL(,,)λθ=E(,,)()λLθ2⋅Pλ⋅dλ(11)的检偏器的琼斯矩阵为：CLiTotal∫CLi沿X轴线偏光检偏器：0由式(1)求出光源通过晶体后的斯托克斯参量，把计⎡10⎤MX=(6)算结果代入式(2)就可以求出输出光的DOP。⎢00⎥⎣⎦3.数值计算及实验结果沿45°轴线偏光检偏器：首先，我们测量一只1490nm的拉曼泵浦激光器的光谱数据，其光谱如图示。⎡0.50.5⎤(7)Mπ/4=⎢⎥⎣0.50.5⎦左旋圆偏光检偏器：⎡0.5−0.5i⎤MCL=⎢⎥(8)⎣0.5i0.5⎦由光的琼斯矢量计算方法，下面分别计算入射光通过晶体后三种偏振光分量：EX(,,)λLiθ=MX⋅MSn⋅MSn−1...MS1⋅MIFig2:ThespectrumofpumplaserE(,,)λLθ=M⋅MS⋅MS...MS⋅MI(9)π/4iπ/4nn−11由上面所述计算方法，通过MathCAD数学工具软EL(,,)λθ=MCL⋅MS⋅MS...MS⋅MICLinn−11件计算的DOP随YVO4晶体长度及偏振光角度的关系光强度透过率为：如图，我们看到输出光DOP随晶体长度逐渐变小，中2间有变大的波动，同时当偏振光角度为45°时DOP比ILELX(,,)(,,)λiθ=Xλiθ偏振光角度为40°时小。通过模拟计算，我们可以得ILEL(,,)(,,)λθ=λθ2(10)π/4iπ/4i到如果需要得到DOP<10％的消偏效果，只需设计2ILELCL(,