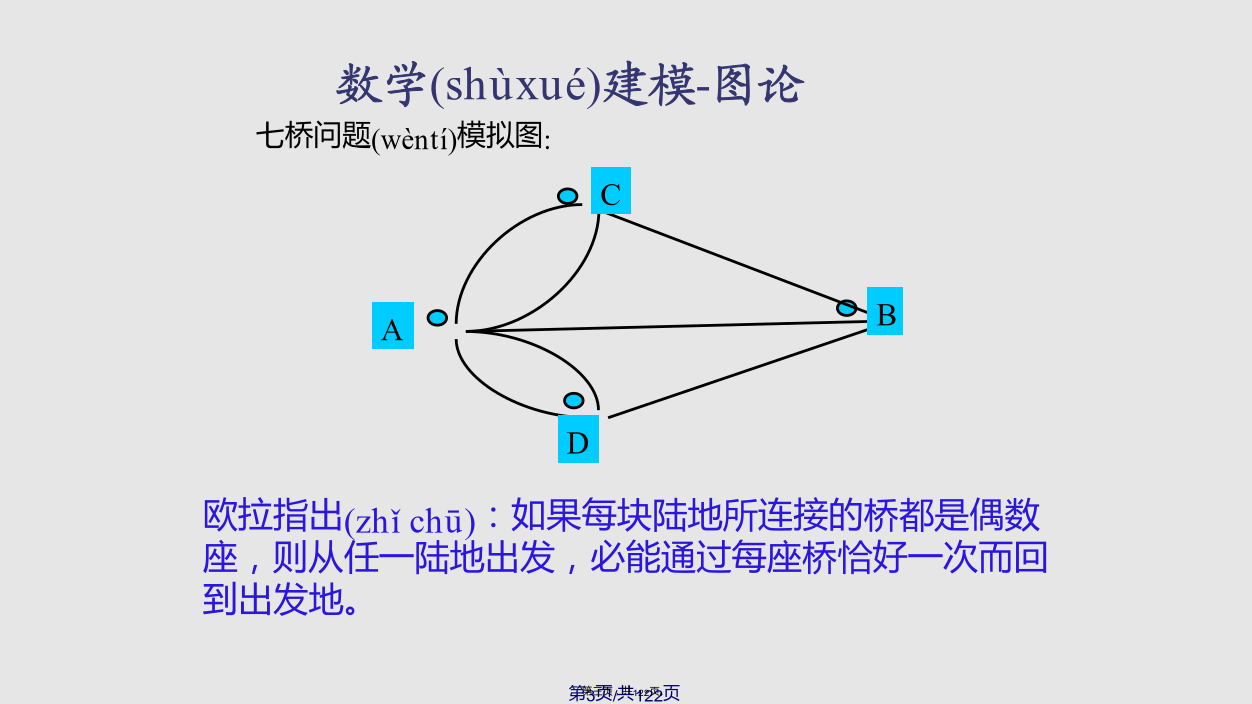
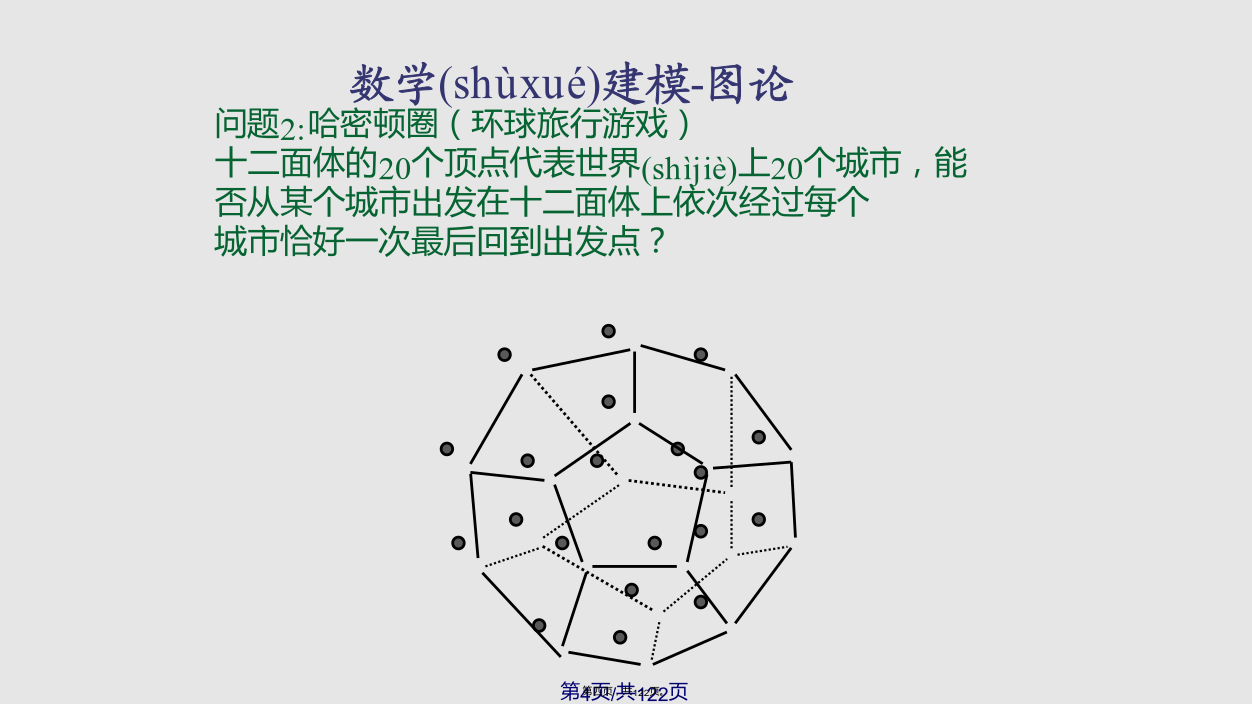
图论方法(fāngfǎ)专题七桥问题(wèntí)模拟图:问题(wèntí)3:四色问题(wèntí)1847年德国的克希霍夫(G.R.Kirchoff)将树的概念和实践(shíjiàn)利用于工程技巧的电网络方程组的研究；1857年英国的凯莱(A.Cayley)也提出了树的概念，并运用于有机化合物的分子构造的研究中；1936年匈牙利的数学家哥尼格(D.Konig)写出了第一本图论专著《有限图与无穷图的理论》，使图论成为一门独立的学科。由于管理、军事、交通运输、计算机和通讯网络等方面的大量问题的出现，大大增进了图论的发展。特别是电子计算机的大量应用，使大规模问题的求解成为可能。实际问题如电网络、交通网络、电路设计、数据结构以及社会科学中的问题所涉及到的图形都是很复杂的，需要计算机的辅助(fǔzhù)才有可能进行分析和解决。目前图论在物理、化学、运筹学、计算机科学、电子学、信息论、经济治理等几乎所有学科领域都有应用。数学(shùxué)建模-图论9一、图的基本概念常用d(v)表示图G中与顶点v关联的边的数目(shùmù),d(v)称为顶点v的度数.与顶点v出关联的边的数目(shùmù)称为出度，记作d+(v)，与顶点v入关联的边的数目(shùmù)称为入度，记作d-(v)。几个(jǐɡè)基本定理：若将图G的每一条边e都对应一个实数(shìshù)F(e),则称F(e)为该边的权,并称图G为赋权图,记为G=(V,E,F).顶点u与v称为连通的，如果(rúguǒ)存在u到v通路，任二顶点都连通的图称为连通图，否则，称为非连通图。极大连通子图称为连通分图。邻接矩阵(jǔzhèn)（结点与结点的关系）关联矩阵(jǔzhèn)（结点与边的关系）路径矩阵(jǔzhèn)（任意两结点之间是否有路径）可达性矩阵(jǔzhèn)直达矩阵(jǔzhèn)等等……1有向图的邻接矩阵A=(aij)n×n（n为结点(jiédiǎn)数）2有向图的权矩阵(jǔzhèn)A=(aij)n×n（n为结点数）3有向图的关联矩阵A=(aij)n×m（n为结点(jiédiǎn)数m为边数）例3：分别(fēnbié)写出右边两图的关联矩阵二、图的矩阵(jǔzhèn)表示该问题用图论中的邻接矩阵解决较为简单易见，令x=t-s，其中，t代表(dàibiǎo)相邻两槽高度之差不为5的锁具数，即：满足限制条件(2)的锁具数，s代表(dàibiǎo)相邻两槽高度之差不为5且槽高仅有1个或2个的锁具数，即：满足限制条件(2)但不满足限制条件(1)的锁具数．我们用图论方法计算t和s.二、图的矩阵表示（应用实例及解法(jiěfǎ)分析）二、图的矩阵(jǔzhèn)表示（应用实例及解法分析）又令二、图的矩阵表示（应用实例解法(jiěfǎ)分析）二、图的矩阵(jǔzhèn)表示（应用实例及解法分析）二、图的矩阵表示（应用实例(shílì)及解法分析）二、图的矩阵表示（应用实例及解法(jiěfǎ)分析）二、图的矩阵表示（应用实例(shílì)及解法分析）二、图的矩阵(jǔzhèn)表示（应用实例及解法分析）二、图的矩阵表示（应用实例及解法(jiěfǎ)分析）二、图的矩阵表示(biǎoshì)（应用实例及解法分析）二、图的矩阵表示（应用实例(shílì)及解法分析）若将图G的每一条(yītiáo)边e都对应一个实数F(e),则称F(e)为该边的权,并称图G为赋权图,记为G=(V,E,F).重要(zhòngyào)性质：设有给定(ɡěidìnɡ)连接若干城市的公路网，寻求从指定城市到各城市的最短路线。3839404142434445Floyd算法(suànfǎ)5455565758596061（2）答案(dáàn)：由于T=2小时,t=1小时,V=35公里/小时,需访问现在尝试(chángshì)将顶点分为4组.分组的原则：除遵从/表3符号说明：加有底纹的表示(biǎoshì)前面经过并停留过,顶点u与v称为连通(liántōng)的，如果存在u-v通路，任二顶点都连通(liántōng)的图称为连通(liántōng)图，否则，称为不连通(liántōng)图。极大连通(liántōng)子图称为连通(liántōng)分图。定理设G是具有n个顶点的图，则下述命题(mìngtí)等价：若任意一个连通的图G=<V,E>的生成子图T=<V’,E’>(V’=V,E’为E的子集(zǐjí))为树,这棵树T称为图G的生成树.怎样(zěnyàng)找出最小生成树？？？步骤(bùzhòu)如下：例用Kruskal算法(suànfǎ)求下图的最小树.73747576777879称经过(jīngguò)图G=(V,E)的每条边恰好一次的路为Euler路径，经过(jīngguò)G的每条