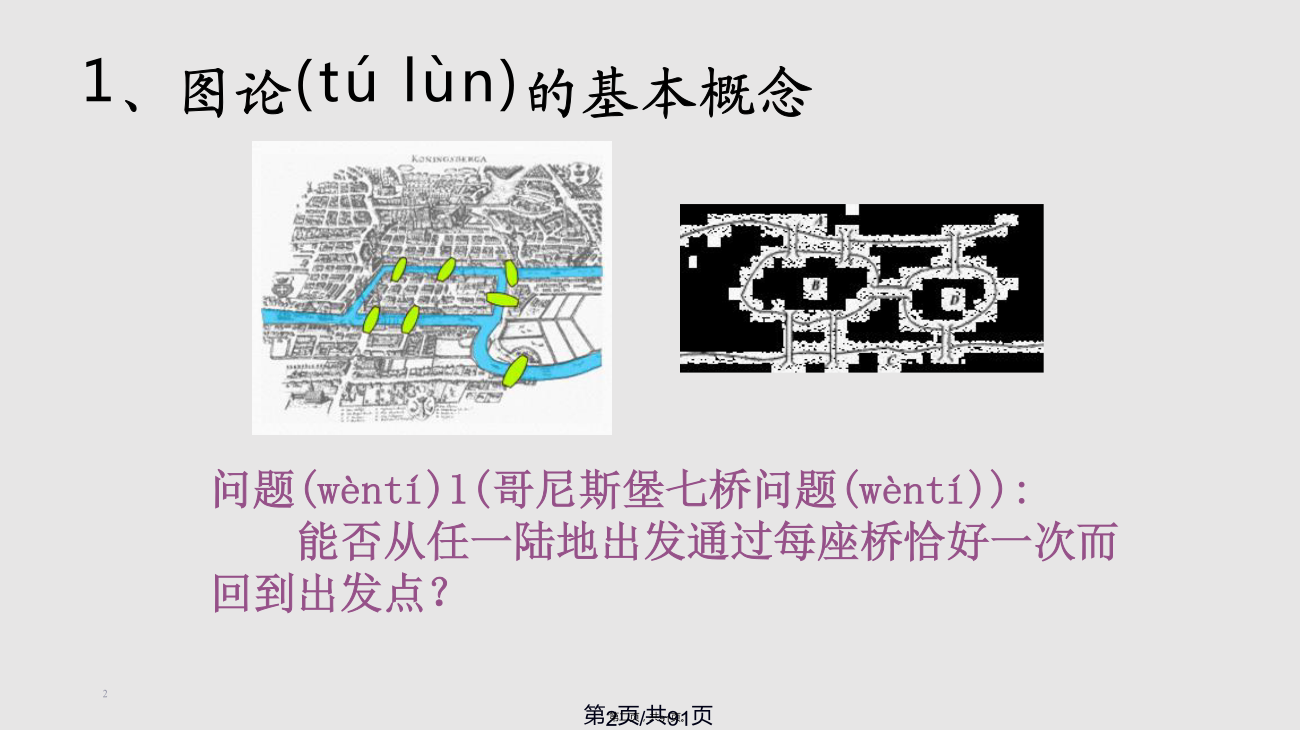
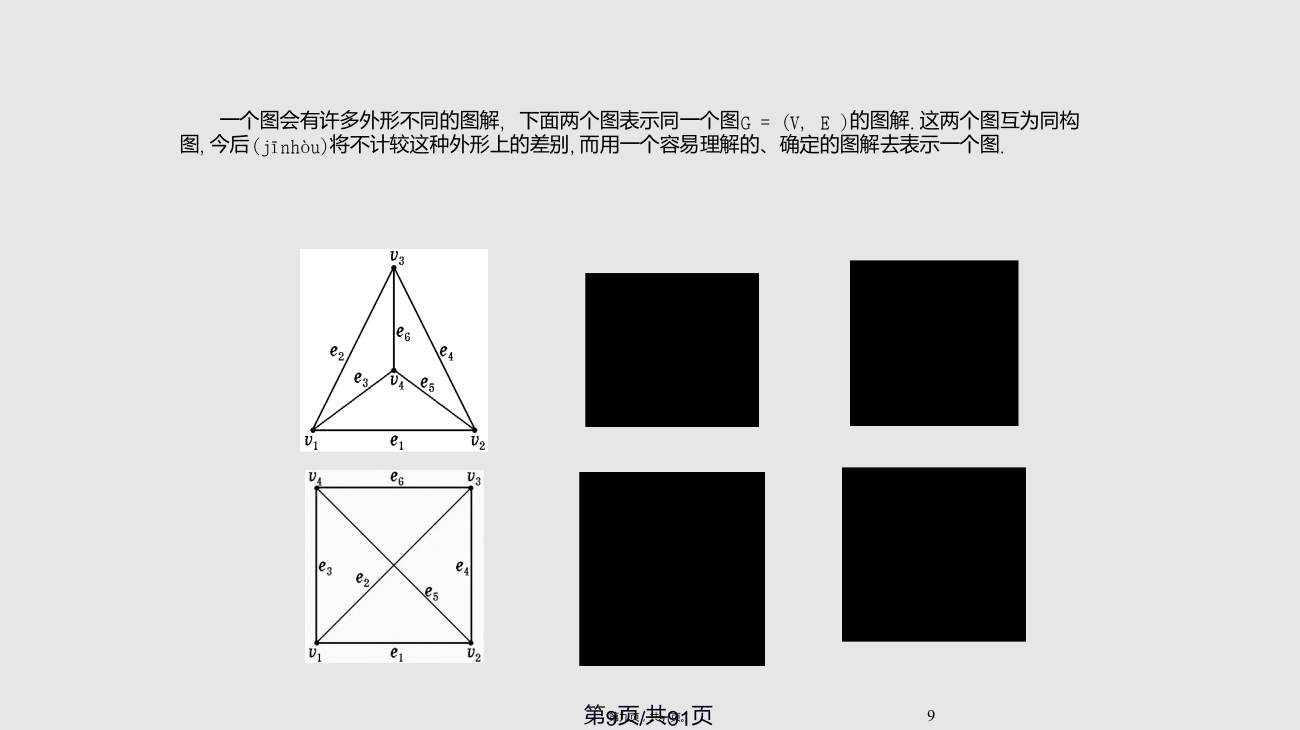
图论(túlùn)模型1、图论(túlùn)的基本概念345图的定义(dìngyì)7891011我们(wǒmen)今后只讨论有限简单图：13常用(chánɡyònɡ)的图例Ramsey问题(wèntí)例Ramsey问题(wèntí)例Ramsey问题(wèntí)例过河问题(wèntí)例过河问题(wèntí)例过河问题(wèntí)图的矩阵(jǔzhèn)表示222324252、最短路径(lùjìng)算法27Dijkstra算法(suànfǎ)Dijkstra算法（求a点到其他(qítā)点的最短路径）改进(gǎijìn)Dijkstra算法（求a点到其他点的最短路径）例求下图中A点到其他(qítā)点的最短路.Floyd算法(suànfǎ)（求任意两点的最短路径）例求下图中任意(rènyì)两点间的最短路.例设备(shèbèi)更新问题35363、最小生成(shēnɡchénɡ)树Kruskal算法(suànfǎ)求最小生成(shēnɡchénɡ)树Prim算法(suànfǎ)例选址(xuǎnzhǐ)问题424、遍历性问题(wèntí)解法：若本身就是欧拉图，则直接可以找到一条欧拉巡回就是本问题的解。若不是欧拉图，必定有偶数个奇度数结点，在这些奇度数点之间添加一些边，使之变成欧拉图，再找出一个欧拉巡回。具体(jùtǐ)解法：Fleury算法+Edmonds最小对集算法三、哈密尔顿图G=(V,E)为一连通无向图经过G中每点一次且正好一次的路径称为哈密尔顿路径；经过G中每点一次且正好一次的回路称为哈密尔顿回路；存在哈密尔顿回路的图称为哈密尔顿图。四、旅行商问题（TSP－TravelingSalesmanProblem）一名推销员准备前往若干城市推销产品。如何为他（她）设计一条最短的旅行路线？即：从驻地出发，经过每个城市恰好一次，最后返回驻地（最小哈密尔顿回路）对于n个节点的旅行商问题，n个节点的任意一个(yīɡè)全排列都是问题的一个(yīɡè)可能解（假设任意两个点之间都有边）。G个节点的全排列有(n-1)!个，因此间题归结为在(n-1)!个回路中选取最小回路。TSP问题的解法属于NP完全问题，一般只研究其近似解法最邻近算法(1)选取任意一个点作为(zuòwéi)起始点,找出与该点相关联的权重最小的边,形成一条初始路径.(2)找出与最新加入到路径中的点相关联的权重最小的边加入到路径中,且要求不再路径中产生回路.(3)重复(2)直到所有的结点都加入到路径中.(4)将起点和最后加入的结点之间的边加入到路径中,形成Hamilton回路.其他数值算法：人工神经元方法，遗传算法等等5、二分(èrfēn)图与匹配48工作安排(ānpái)问题之一5051例求下图所示二部图G的最大匹配(pǐpèi)5354工作安排(ānpái)问题之二56576、网络(wǎngluò)流问题5960最小费用(fèiyong)流问题6263647、关键(guānjiàn)路径问题（拓扑排序）PT(Potentialtaskgraph)图676869关键路径(lùjìng)(最长路径(lùjìng))算法7172737475PERT图778、系统监控模型(móxíng)系统监控问题(wèntí)之一最大独立(dúlì)点集最小控制(kòngzhì)集系统监控问题(wèntí)之二最小点覆盖(fùgài)、最大独立点集和最小控制集的关系9、着色(zhuósè)模型对偶(duìǒu)图物资储存(chǔcún)问题时间表问题(wèntí)88着色(zhuósè)方法最大度数优先(yōuxiān)的Welsh-Powell算法91