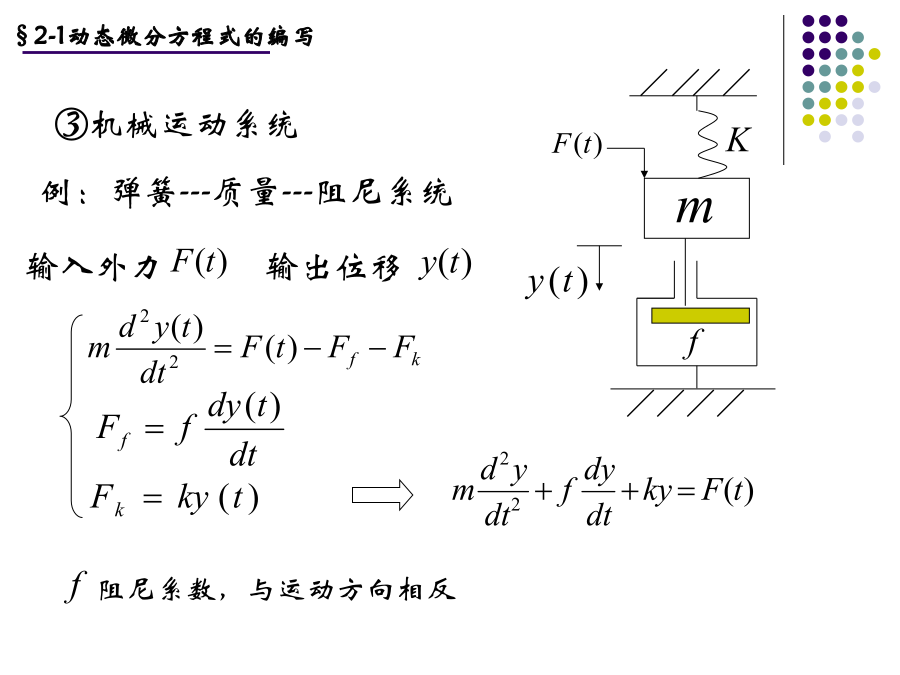
§2-1动态微分方程式的编写§2-2非线性数学模型的线性化2.数学描述设系统的输入为x(t),输出为y（t），且满足y(t)=f(x),其中f(x)为非线性函数。设t=t0时，x=x0,y=y0为系统的稳定工作点（x0,y0）,§2-2非线性数学模型的线性化也即：即有：自动控制系统的典型输入信号§3-1控制系统的暂态响应分析§3-1控制系统的暂态响应分析§3-1控制系统的暂态响应分析拉普拉斯变换(Laplace变换)在数学中，为了把较复杂的运算转化为较简单的运算，常常采用一种变换手段，所谓积分变换，就是通过积分运算把一个函数变成另一个函数的变换。积分变换包括拉普拉斯（Laplace）变换和傅立叶（Fourier）变换。这里只研究Laplace变换，讨论他的定义、性质及其应用。在所确定的某一域内收敛,则由此积分所确定的函数可写为二、一些常用函数的拉普拉斯变换例3求函数的拉氏变换例5正弦函数是周期为（1）线性性质《自动控制原理》国家精品课程浙江工业大学自动化研究所四拉氏反变换1利用拉普拉斯变换表和性质求拉普拉斯逆变换《自动控制原理》国家精品课程浙江工业大学自动化研究所2.用留数法分解部分分式例2已知II.当有重根时例5已知常系数线性微分方程的拉普拉斯变换解法例17求微分方程用L变换方法解线性常微分方程课后作业