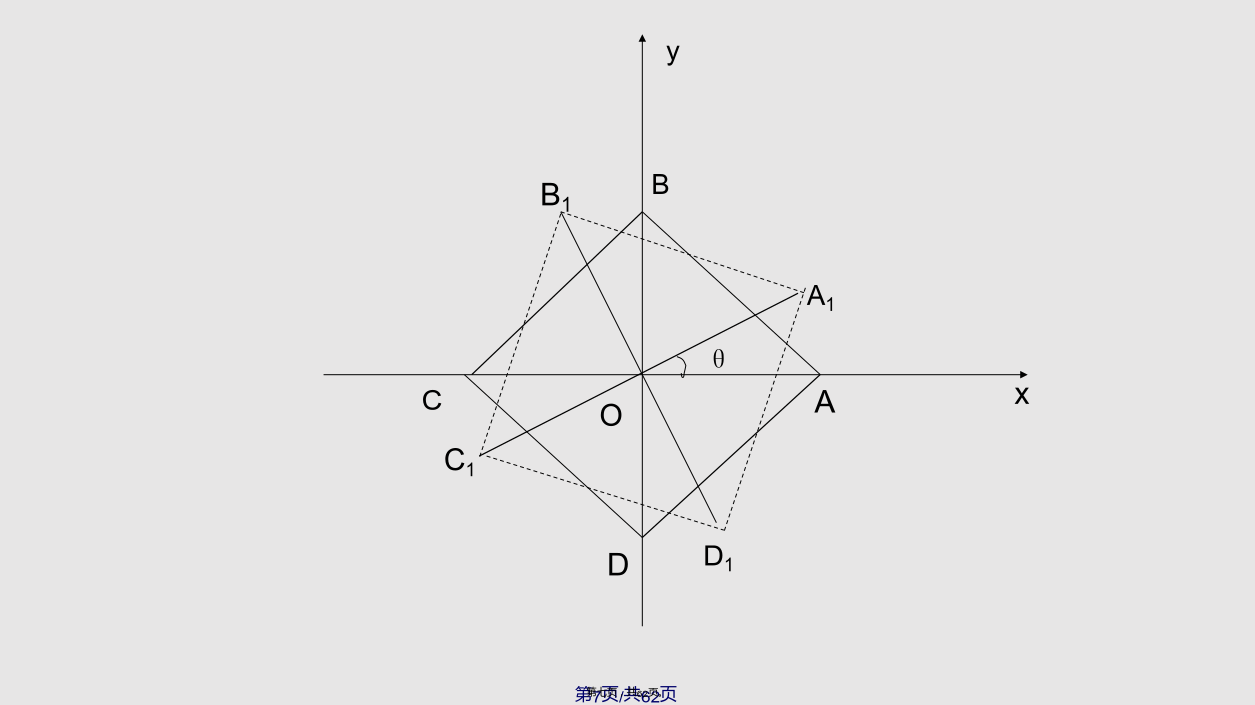
数学(shùxué)建模建模的一般(yībān)步骤数学(shùxué)建模的原则一、简单的数学建模案例(ànlì)介绍2.椅子(yǐzi)能在不平的地面上放稳吗？3、对于椅脚的间距和椅腿的长度而言，地面是相对平坦的，使椅子在任何位置至少(zhìshǎo)有三只脚同时着地。其次要把椅脚着地用数学符号表示出来。可用某个变量表示椅脚与地面的竖直距离，当其为零时就是椅脚着地了。由于正方形的中心(zhōngxīn)对称性，只要设两个距离函数就行了。记A、C两脚与地面距离之和为f(θ)，B、D与地面距离之和为g(θ)（f(θ)，g(θ)非负）。由假设2，f和g都是连续函数。由假设3，椅子在任何位置至少有三只脚着地，所以对于任意的θ，f(θ)，g(θ)中至少有一个为零。当θ=0，时不妨设g(θ)=0，f(θ)〉0，这样，改变椅子的位置使四只脚同时着地，就归结为证明下列的数学命题：/3.人狗鸡米问题(wèntí)由于人、狗、鸡、米是4种互不相同的事物，用四维向量来描述。然后用向量的代数运算来进行(jìnxíng)分析研究。再给出决策向量(xiàngliàng)，将船的一次运载也表成向量(xiàngliàng)，当一物在船上记相应的分量为1，否则为0，称为决策向量(xiàngliàng)。本系统决策向量(xiàngliàng)有4个：（1，0，1，0）（1，1，0，0）（1，0，0，1）（1，0，0，0）（1）状态(zhuàngtài)的可取运算：/（2）将可取状态的点与运算得到的可取状态的点连接(liánjiē)。得到下面的图（1，1，1，1）在上图中找出一条从点（1，1，1，1）到点（0，0，0，0）的路径(lùjìng)，则每条路径(lùjìng)就是一个解。由上图可知，有两个解，都是经7次运算，均为最优解。4.夫妻(fūqī)过河问题记第k次过河前南岸的男子(nánzǐ)数为xk,女子数为yk,k=1,2,…,xk,yk=0,1,2,3,则状态向量可表为(xk,yk),其可取状态或允许状态有10个：(0,0),(0,1),(0,2),(0,3),(3,0)(3,1),(3,2),(3,3）,(1,1),(2,2)这样，夫妻过河问题(wèntí)就归结成求由状态(3,3)经奇数次允许决策到达状态(0,0)的状态转移过程。第2次过河是将(3,2),(3,1),(2,2)分别与决策向量进行运算，只须k=2，如此(rúcǐ)下去，不难验证，经11次可取运算三对夫妻就可全部按规则过河。利用上面的模型编制程序，就易在计算机上实现(shíxiàn)求解。2、图解法这里介绍的是一种规格化的方法。所建立的多步决策模型可以用计算机求解，从而具有推广的意义。适当地设置状态和决策，确定状态转移(zhuǎnyí)律，建立多步决策模型，是有效地解决很广泛的一类问题的方法。二、微分方程(wēifēnfānɡchénɡ)模型1、传染病模型(móxíng)（一）问题(wèntí)的提出传染病的研究涉及(shèjí)这些疾病的发病机理、临床表现、诊断和治疗方法，这是传染病学的研究重点。那么传染病的传播规律是什么呢？它是否会一直持续下去而无法彻底消灭呢？被传染的人数与哪些因素有关？如何预报传染病高潮的到来？为什么同一地区一种传染病每次流行时，被传染的人数大致不变？对传染病传播进行研究，首先要了解不同的传染病传播过程的特点。这里只能在较一般的情形下，按照传染病一般的传播机理建立数学模型。（二）最简单(jiǎndān)的模型于是，得下列(xiàliè)常微分方程数学模型：其解为：这个结果表明，感病者将按指数规律无限增加，当时，。显然与实际情况不符。事实上，一个地区的总人数可视为常数（不考虑传染病传播期间出生和迁移的人数）。在传染病传播期间，一个感病者单位时间能传染的人数k0是改变的。初期k0较大，随着病人感病者增多，易感者较少，传染机会也将减少，于是k0也会变小(biànxiǎo)。所以应该对该模型的假设进行修改。（三）SI模型(móxíng)易感者接触感病者的机会显然与易感者和感病者的人数成正比，记比例系数为k，称为传染系数，它表示单位时间内，一个感病者可以传染kS(t)个易感者，使之成为感病者。可得关于(guānyú)疾病传染的SI模型：这儿的I0为初始时刻感病者在人群中所占的比例。利用分离(fēnlí)变量法，其解为：以及对I(t)关于t求导，即可得到(dédào)感病者增长的速度（即疾病传播的速度）为图1与图2分别(fēnbié)是I(t)和dI/dt的变化曲线。图2称为传染病曲线。由于(yóuyú)当I=1/2,即时，，从而达最大值。即，当t=tm时，疫情最为猛烈(měngliè)，病人增加的速度最快，