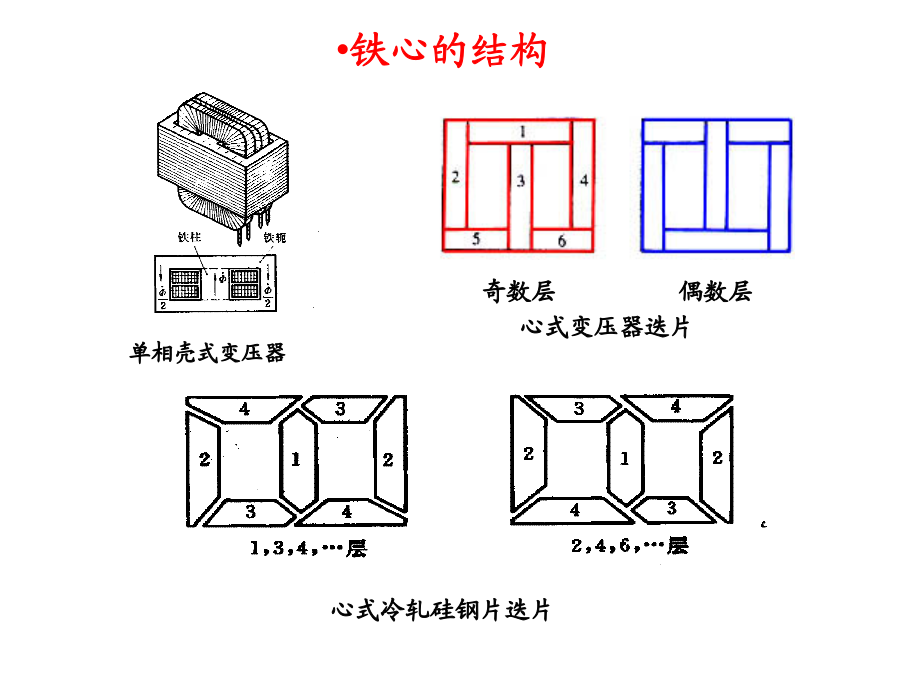
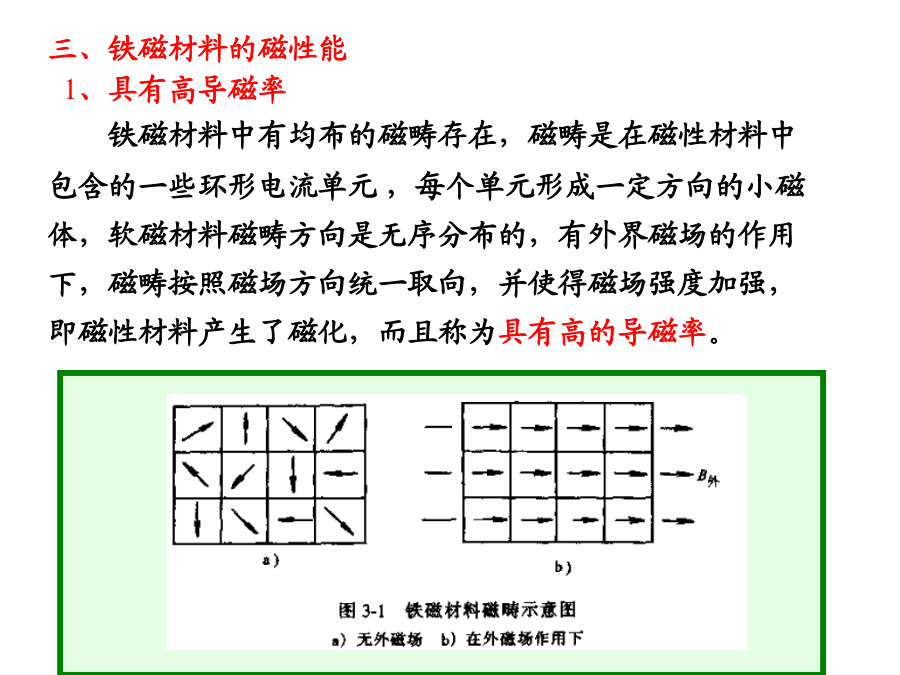
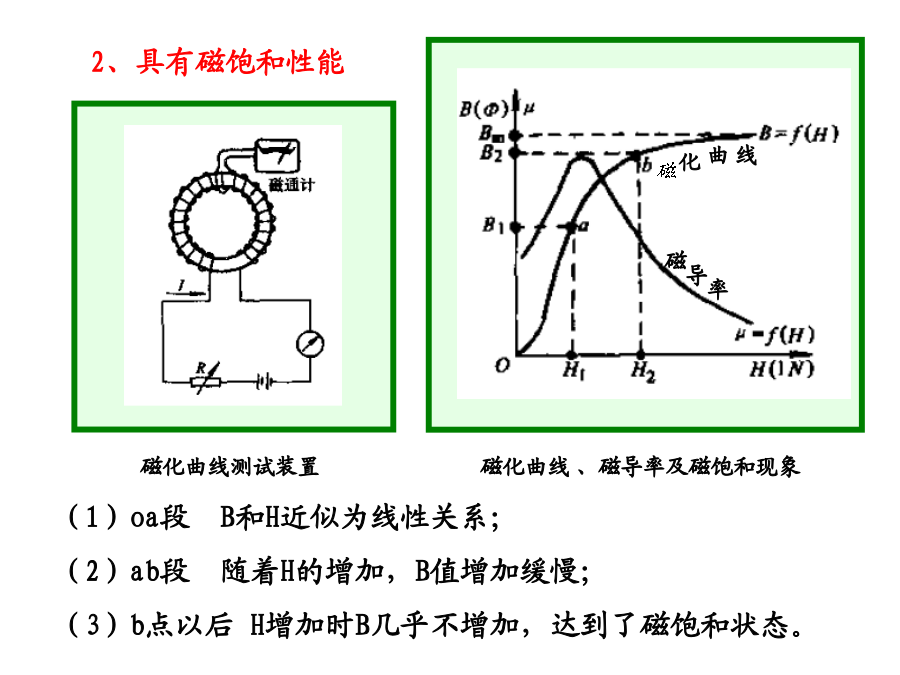
第三章弧焊变压器变压器实例一、变压器的基本结构铁心的结构二、基本物理量相对磁导率μr：某种物质的磁导率与真空中磁导率的比值四、铁磁材料中的能量损耗六、绝缘系统、冷却方式、允许温升2、冷却：3、温升：弧焊变压器设变压器中铁心中空载磁通量瞬时值Ф0按照正弦规律变化，幅值为Ф0m，初相角为零，有Ф0=Ф0msinωt，按照电磁感应定律公式分析得出初级绕组的感应电动势瞬时值表达式为：e10=-N1ωФ0mcosωt=N1ωФ0msin(ωt﹣90°)（3—1）次级绕组的感应电动势瞬时值表达式为：e10=-N2ωФ0mcosωt=N2ωФ0msin(ωt﹣90°)由上式可知，感应电动势总是滞后于磁通量90°的相位角。由上面瞬时值表达式可以得到有关有效值表达式：E10=4.44fN1Ф0m=4.44fN1BmSFeE20=4.44fN2Ф0m=4.44fN2BmSFeU1=4.44fN1Ф1m=4.44fN1BmSFeE10/U1=Φ0m/Φ1m=Φ0/Φ1=KM有漏磁时，空载电压只是由耦合磁通Ф0(主磁通)建立的；没有漏磁时，让上页最后的式中耦合系数KM=1得到U0=E20=U1（N2/N1）变压器空载时有漏磁，在一次绕组中也就产生了漏感电动势或感抗压降。根据克氏第二定律，可以写出变压器一次电路的复数电压方程式为：负载条件下的电磁关系在负载状态等效电路图次级回路中加入电抗器k,并将初级回路参数X1、R1折算到次级为X1´，R1´，则通过推导或直接列写，均可得到完整的次级回路复数电压平衡方程式：Uf=U0－jI2(X1´+X2+XK)－I2(R1´+R2+RK)(1)令上式中的X1´+X2=XL，考虑到电阻项(R1´+R2+RK)的值很小可以忽略，而且I2=If(If为负载电流或电弧电流)则(1)式简化为Uf=U0－jIf(XL+XK)(2)再令XZ＝XL+XKXZ为折算到次级回路的变压器总漏抗，最后得到简化的次级回路复数电压平衡方程式：Uf=U0－jIfXZ(3)结论：1.式(1)、(2)、(3)是弧焊变压器的复数电压平衡方程式，也是弧焊变压器的外特性方程式，式(3)是简化的外特性方程式。2.增大漏电感X1和X2都会使外特性下降得更陡。3.在二次电路中串联附加电抗器XK，也可以获得下降外特性4.根据简化的复数电压平衡方程式得到负载电流有效值显式表达式：If=(U02-Uf2)1/2/(XL+Xk）=(U02-Uf2)1/2/XZ(4)由(4)式可知，改变焊接变压器的漏电感XL或附加电抗器电感XK都可以调节焊接电流If。3、弧焊变压器的等效电路图：根据上述弧焊变压器的电压平衡方程式（1）或者（3），可以画出下面完整的或者简化的折算到次级回路的等效电路图：4、利用上述简化的复数电压方程式(3)可以做出相应的电压矢量图如右图所示。由右图所表示的几何关系可以写出电流有效值显式表达式：二、弧焊变压器的分类根据获得下降外特性的方法不同可分为串联电抗器式、增强漏磁式。(一)串联电抗器式由正常漏磁(漏磁很少，可忽略)的变压器，另外串联一个单独的电抗器构成，按结构不同又分为：1．分体式变压器和电抗器是两个独立的个体。BP—3X500型多站式弧焊变压器属于此类，2．同体式变压器与电抗器铁心组成一体，二者之间不但有电的串联，还有磁的联系。BX2系列弧焊变压器属于此类。(二)增强漏磁式这类变压器增大自身的漏抗，不必再串联单独的电抗器。按增强和调节漏抗的方法不同又可分为：1．动铁心式在一、二次绕组间设置有可移动铁心的磁分路，以增强和调节漏磁。BXl系列弧焊变压器即属此类。2．动绕组式通过增大一、二次绕组之间距离来增强漏磁，改变绕组之间距离进行调节。BX3系列弧焊变压器属于此类。3．抽头式将一、二次绕组进行不同程度的分置来增加和调节漏磁。首先对绕组进行多点抽头，通过抽头置换改变初次级绕组的分置程度，也就是改变初次级绕组的耦合程度，来调节漏抗。BX6—120型弧焊变压器属于此类。