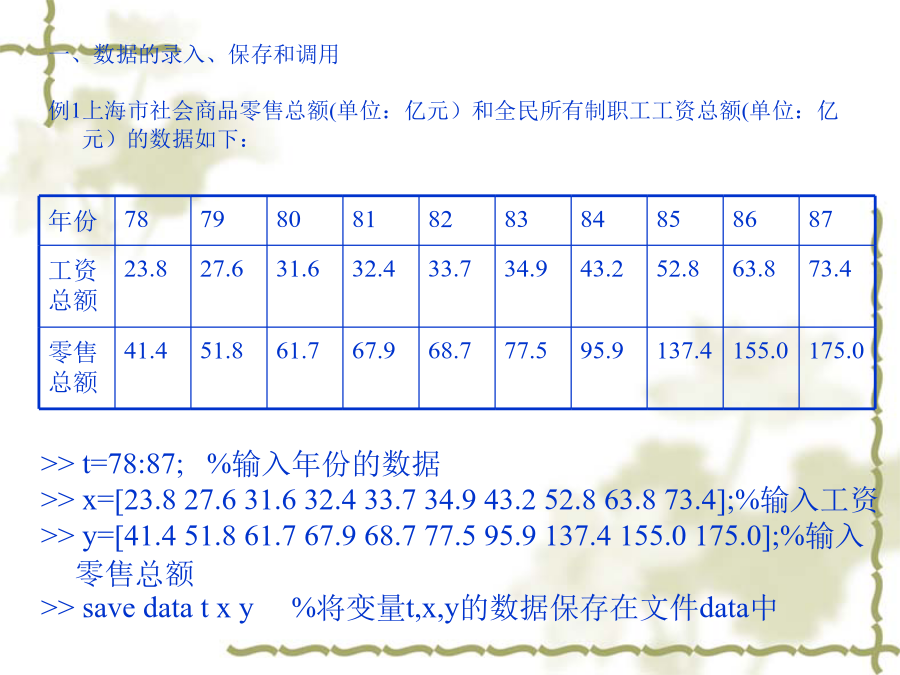
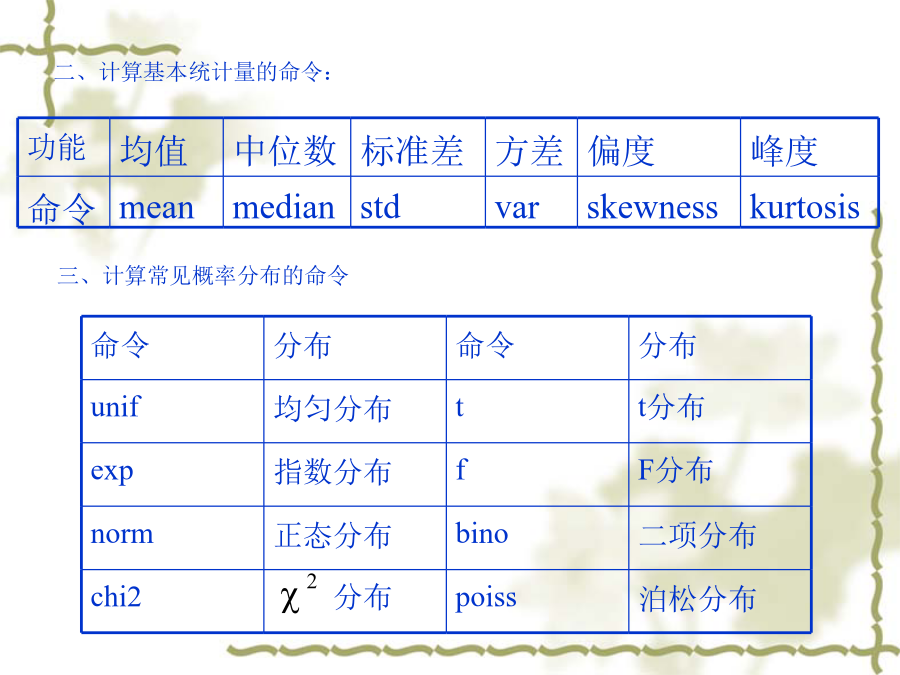
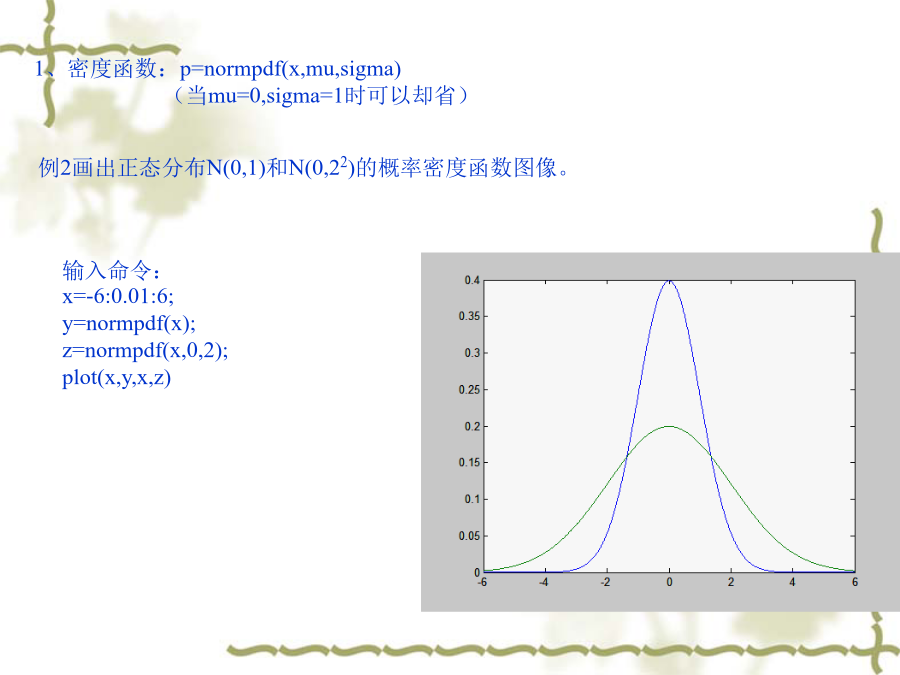
一、数据的录入、保存和调用loaddata方法2：用矩阵形式输入和保存数据二、计算基本统计量的命令：工具箱对每一种分步都提供了五类函数，其命令字符为例2画出正态分布N(0,1)和N(0,22)的概率密度函数图像。2、概率分布：P=normcdf(x,mu,sigma)3、逆概率分布x=norm(P,mu,sigma)即求出x，使得P(x<1)=P,此命令可用来求分位数。例6计算均值100，标准差10的正态分布随机变量的概率0.01的分位数。5、随机数生成：normrnd(mu,sigma,m,n)产生m×n阶的正态分布随机数生成。其它分布举例：（1）它的尺寸在[19,22]区间内的概率为四、参数估计的命令：其它分布的参数估计：（1）[muhat,muci]=expfit(X,alpha)求指数分布的数据X的均值的点估计和区间估计；（2）[lambdahat,lambdaci]=poissfit(X,alpha)求泊松分布的数据X的参数λ的点估计和区间估计例10为估计一件物体的重量μ和方差σ2，将其称了10次，得到的重量（单位：千克）为：10.1,10,9.8,10.5,9.7,10.1,9.9,10.2,10.3,9.9假设所称出的物体总量服从N(μ,σ2),求重量μ和方差σ2置信系数0.95置信区间。假设检验：2、总体方差sigma2未知时，总体均值得检验使用t-检验[h,sig,ci]=ttest(x,m,alpha,tail)tail=0,检验假设“x的均值等于m”tail=1,检验假设“x的均值大于m”tail=-1,检验假设“x的均值小于m”tail的缺省值为0，alpha的缺省值为0.05返回值h=1表示可以拒绝假设，h=0表示不可以拒绝假设sig为假设成立的概率，ci为均值的1-alpha置信区间3、两个总体均值得检验使用t-检验[h,sig,ci]=ttest2(x,y,alpha,tail)tail=0,检验假设“x的均值等于y的均值”tail=1,检验假设“x的均值大于y的均值”tail=-1,检验假设“x的均值小于y的均值”tail的缺省值为0，alpha的缺省值为0.05返回值h=1表示可以拒绝假设，h=0表示不可以拒绝假设sig为假设成立的概率，ci为均值的1-alpha置信区间例10已知某炼铁厂的铁水含碳量在正常情况下服从正态分布N(4.55,0.112).某日测得5炉铁水含碳量如下:4.28,4.40,4.42,4.35,4.37.如果标准差不变,该日铁水的平均含碳量是否显著偏低?(取=0.05)例11某厂生产镍合金线，其抗拉强度的均值为10620(kg/mm2)今改进工艺后生产一批镍合金线，抽取10根,测得抗拉强度(kg/mm2)为:10512,10623,10668,10554,10776,10707,10557,10581,10666,10670.认为抗拉强度服从正态分布,取=0.05,问新生产的镍合金线的抗拉强度是否比过去生产的合金线抗拉强度要高?命令：x=[10512,10623,10668,10554,10776,10707,10557,10581,10666,10670];[h,sig,ci]=ttest(x,10620,0.05,0)例12比较甲,乙两种安眠药的疗效。将20名患者分成两组,每组10人.其中10人服用甲药后延长睡眠的时数分别为1.9,0.8,1.1,0.1,-0.1,4.4,5.5,1.6,4.6,3.4;另10人服用乙药后延长睡眠的时数分别为0.7,-1.6,-0.2,-1.2,-0.1,3.4,3.7,0.8,0.0,2.0.若服用两种安眠药后增加的睡眠时数服从方差相同的正态分布.试问两种安眠药的疗效有无显著性差异？命令：x=[1.9,0.8,1.1,0.1,-0.1,4.4,5.5,1.6,4.6,3.4];y=[0.7,-1.6,-0.2,-1.2,-0.1,3.4,3.7,0.8,0.0,2.0];[h,sig,ci]=ttest2(x,y,0.10,0)