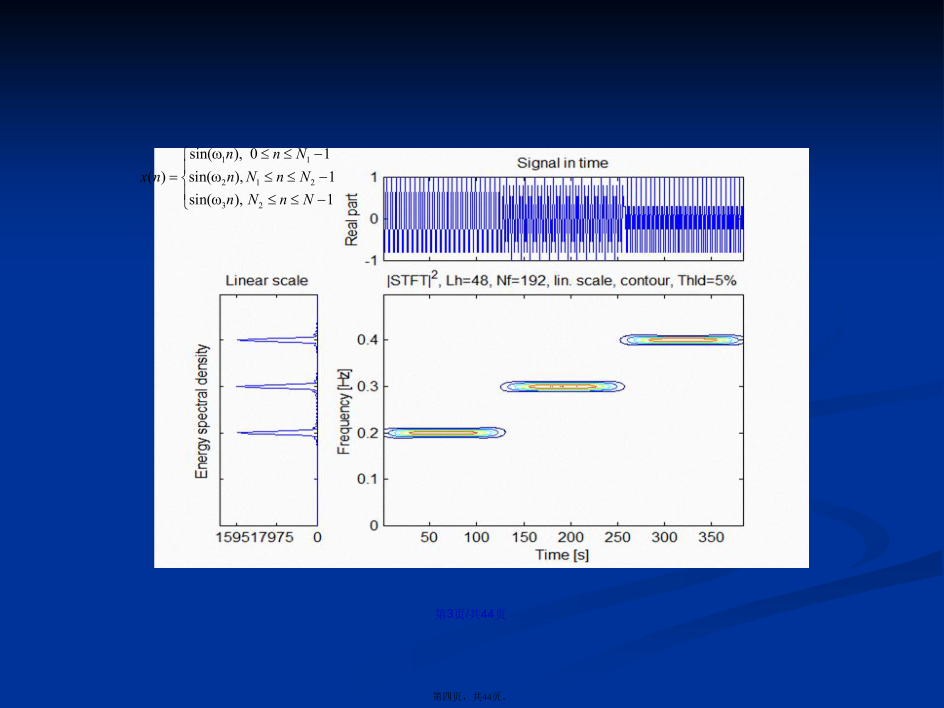
会计学5.1引言1、引言(yǐnyán)2、解析(jiěxī)信号Hilbert变换器的传输(chuánshū)函数为Z(f)=S(f)+jH(f)S(f)=S(f)［1+jH(f)］3、瞬时(shùnshí)频率4、不确定(quèdìng)原理5.2短时傅里叶变换(biànhuàn)/图2.1.3窗函数无限宽时STFT缺少时域定位功能注：见胡广书《现代(xiàndài)信号处理教程》图2.1.3图2.1.4窗函数无限窄时STFT缺少频域定位功能注：见胡广书《现代信号处理(xìnhàochǔlǐ)教程》图2.1.4由于受不定原理的制约，窗函数的有效时宽和带宽不可能同时任意小，窗宽应该(yīnggāi)与信号的局域平稳长度相适应。对时间分辨率和频率分辨率只能取一个折中，一个提高了，另一个就必然要降低，反之亦然。谱图：一般把短时傅里叶变换模的平方称为谱图，它是一种能量分布函数(hánshù)，不服从线性叠加原理，两个信号之和的谱图并不等于它们分别的谱图的和，还存在第三项即交叉项。5.3小波变换(biànhuàn)1、引言短时傅立叶变换在时频平面各处的分辨率都相同，可以用时频平面的相等网格(wǎnɡɡé)表示。小波基函数的包络随尺度参数的变化(biànhuà)而变化(biànhuà)，可以实现时频平面的多分辨率分析。2、连续小波变换（CWT）连续小波变换的定义设x(t)是平方可积函数，记作，则x(t)的连续小波变换可以定义为：定义式的说明(shuōmíng)：（1）基小波函数可能为复函数，例如Morlet小波的表达式为（4）在ψab前面所加的因子的作用是保证在不同(bùtónɡ)的尺度因子下的小波函数的能量保持一致。设E=∫|ψ(t)|2dt作为基本小波的能量，则对基本小波进行移位和伸缩后得到的ψab(t)的能量为连续小波变换(biànhuàn)的频率域表达式在定义了连续小波变换(biànhuàn)后，对该表达式进行傅里叶变换(biànhuàn),小波变换的特点小波变换的时频关系受不确定原理的制约，在时频平面(píngmiàn)上的分析窗是可调的，但分析窗的面积保持不变。当用较小的a对信号(xìnhào)作高频分析时，实际上是用高频小波对信号(xìnhào)作细致观察;当用较大的a对信号(xìnhào)作低频分析时，实际上是用低频小波对信号(xìnhào)作概貌观察。注：见张贤达《现代(xiàndài)信号处理》图6.5.35.4Wigner-Ville分布(fēnbù)(WVD)引言(yǐnyán)时频分布(fēnbù)的定义二次叠加原理(yuánlǐ)设对于有p个分量(fènliàng)的信号，二次叠加原理用下式表示：Wigner-Ville分布(fēnbù)的定义z(t)在频率域的WVD分布定义(dìngyì)如下:5.5Cohen类时频分布(fēnbù)1、模糊函数对瞬时(shùnshí)相关函数kz(t,τ)=z(t+τ/2)z*(t-τ/2)关于时间t作傅里叶反变换，则得到模糊函数的时域定义为模糊函数(hánshù)和WVD之间的关系：WVD是能量(néngliàng)化的时频表示，存在时间边缘特性Pz(t)和频率边缘特性Pz(w)，公式重写如下:模糊函数是相关(xiāngguān)化的时频表示，将模糊函数的定义重写如下:WVD中交叉项的抑制：对信号求模糊函数，由于模糊函数的自项始终在平面的原点处，而交叉项远离原点，故可以设计一个二维低通滤波器，来抑制模糊函数中的交叉项；对滤波后的模糊函数作二维傅立叶变换，得到(dédào)信号的维格纳变换，此时的WVD即是抑制了交叉项的新WVD。2、Cohen类时频分布(fēnbù)当核函数(hánshù)φ(τ,v)=1时，Cohen类时频分布将转换成WVD。由于Wigner分布的核函数(hánshù)是全通函数(hánshù)，它对AF的互项无抑制作用，因此，其WD也就存在着较大的交叉项。消除干扰项的方法：应该选择平面上的二维低通函数(hánshù)来作为核函数(hánshù)。