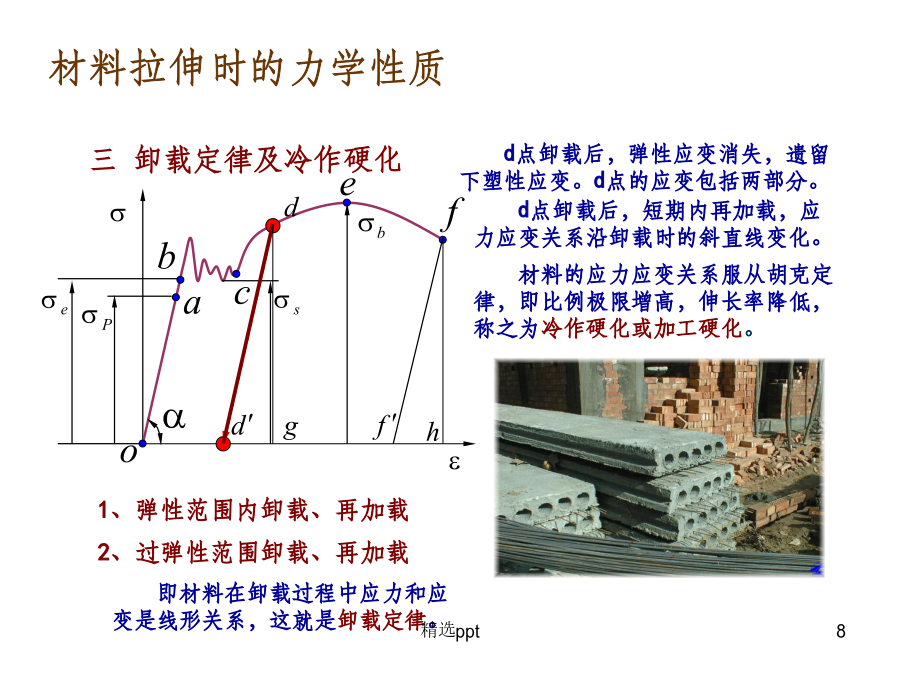
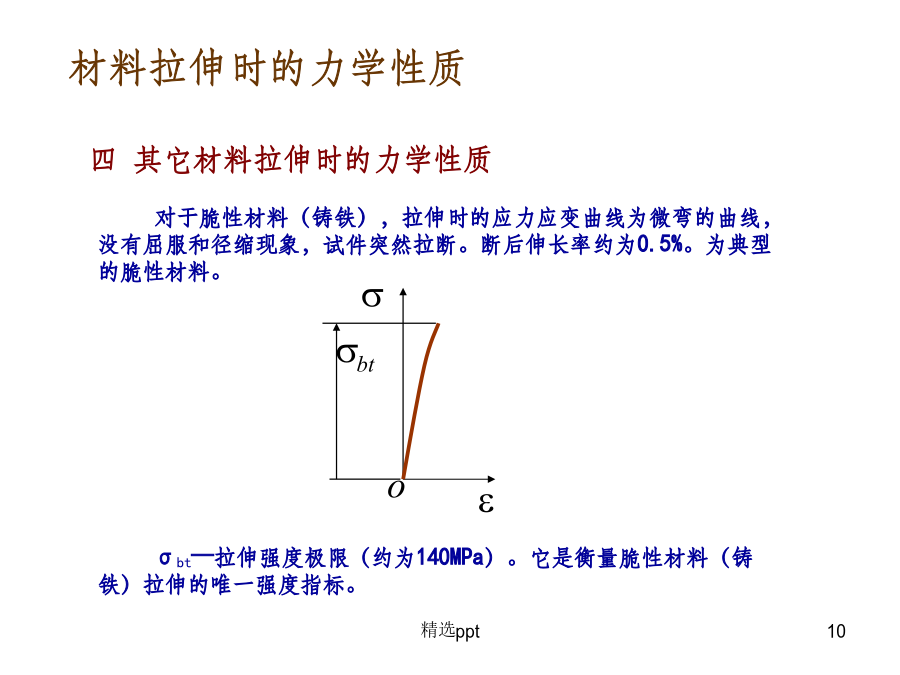
主要内容主要内容§6-1材料拉压时的力学性质材料拉伸时的力学性质材料拉伸时的力学性质材料拉伸时的力学性质材料拉伸时的力学性质材料拉伸时的力学性质材料拉伸时的力学性质材料拉伸时的力学性质材料压缩时的力学性质材料压缩时的力学性质材料压缩时的力学性质其他材料拉伸时力学性能两种材料力学性能的比较强度方面塑性材料:屈服前抗拉和抗压性能基本相同，有屈服现象脆性材料:抗压强度高于抗拉强度，无屈服现象变形方面塑性材料:延伸率和截面收缩率较大，塑性好脆性材料:和较小，塑性差一、材料的破坏形式b．塑性流动（剪切型）——材料有显著的塑性变形（即屈服现象），最大剪应力作用面间相互平行滑移使构件丧失了正常工作的能力。塑性流动主要是由剪应力所引起的。长期以来，人们根据对材料破坏现象的分析，提出过各种各样的假说，认为材料的某一类型的破坏是由某种因素引起的，这种假说就称为强度理论。比如铸铁，其拉伸试样是沿横截面断裂的，扭转圆试样则沿斜截面断裂，两者都是在无明显变形的情况下发生脆性断裂而破坏的。又如低碳试样受拉伸和压缩时，通常会有显著的塑性变形，当构件变形过大时，就失去了正常工作和承载能力。对于低碳钢这类塑性材料，其拉伸和压缩试样都会发生显著的塑性变形，有时并会发生屈服现象，构件也因之而失去正常工作能力，变得失效。由是观之，材料破坏按其物理本质而言，可分为脆断破坏和屈服失效两种类型。同一种材料在不同的应力（受力）状态下，可能发生不同类型的破坏。如有槽和无槽低碳钢圆试样；圆柱形大理石试样有侧压和无侧压下受压破坏。四种常用的强度理论2．第二强度理论（最大伸长线应变理论）该理论能很好地解释石料或混凝土等脆性材料受轴向压缩时沿横向（裂纹呈竖向）发生断裂破坏的现象。铸铁在，且的情况下，试验结果也与该理论的计算结果相近。按照此理论，铸铁在二向拉伸时应比单向拉伸时更安全，这与试验结果不符。同样此理论也不能解释三向均匀受压时，材料不易破坏这一现象。（二）关于塑性流动的强度理论2．第四强度理论（形状改变比能理论）三、强度理论的选用2．强度理论的选用§6-3构件的强度条件§6-4轴向拉伸或压缩时的强度计算根据上述强度条件，可以进行三种类型的强度计算：例1：一直径d=14mm的圆杆，许用应力[σ]=170MPa，受轴向拉力P=2.5kN作用，试校核此杆是否满足强度条件。例2：图示三角形托架,其杆AB是由两根等边角钢组成。已知P=75kN,[σ]=160MPa,试选择等边角钢的型号。解：例2：图示起重机，钢丝绳AB的直径d=24mm，[σ]=40MPa，试求该起重机容许吊起的最大荷载P。解：6.5圆轴扭转时的强度计算强度条件6.6梁的强度计算正应力强度条件正应力强度计算校核强度:截面设计:确定许可荷载:梁的剪应力强度校核剪应力计算公式设计梁时必须同时满足正应力和剪应力的强度条件。对细长梁，弯曲正应力强度条件是主要的，一般按正应力强度条件设计，不需要校核剪应力强度，只有在个别特殊情况下才需要校核剪应力强度。弯曲强度计算的步骤画出梁的剪力图和弯矩图,确定|Q|max和|M|max及其所在截面的位置，即确定危险截面。注意两者不一定在同一截面；根据截面上的应力分布规律，判断危险截面上的危险点的位置，分别计算危险点的应力，即max和max（二者不一定在同一截面，更不在同一点）；对max和max分别采用正应力强度条件和剪应力强度条件进行强度计算，即满足max,max采用合理截面形状原则：当面积A一定时,尽可能增大截面的高度,并将较多的材料布置在远离中性轴的地方,以得到较大的抗弯截面模量(附图);可以用比值Wz/A说明,比值越大越合理.直径为h圆形截面:Wz/A=(h3/32)/(h2/4)=0.125h高为h宽为b矩形截面:Wz/A=(bh2/6)/bh=0.167h高为h槽形及工字形截面:Wz/A=(0.27~0.31)h可见,工字形、槽形截面比矩形合理,圆形截面最差。合理安排梁的支座和荷载目的:减小梁的最大弯矩外伸梁和简支梁的比较:采用变截面梁目的:节省材料和减轻自重理想情况:变截面梁各横截面上最大正应力相等等强度梁:例题3图示简支工字钢梁，材料许用应力为。试按强度选择工字钢型号。解：1）绘制Q、M图，选择危险截面C，D2）按第一强度理论初步选定截面型号：由得选用28a号工字钢，W=5083）按其它强度理论进行校核：I）第三强度理论：I）第三强度理论：满足。II）腹板与翼缘交界处的强度校核：正应力剪应力求得分别为：179.5,0,-68.0Mpa。按第三强度理论：按第四强度理论：均远大于许用应力。应加大截面选28b号工字钢。仿造上述方法