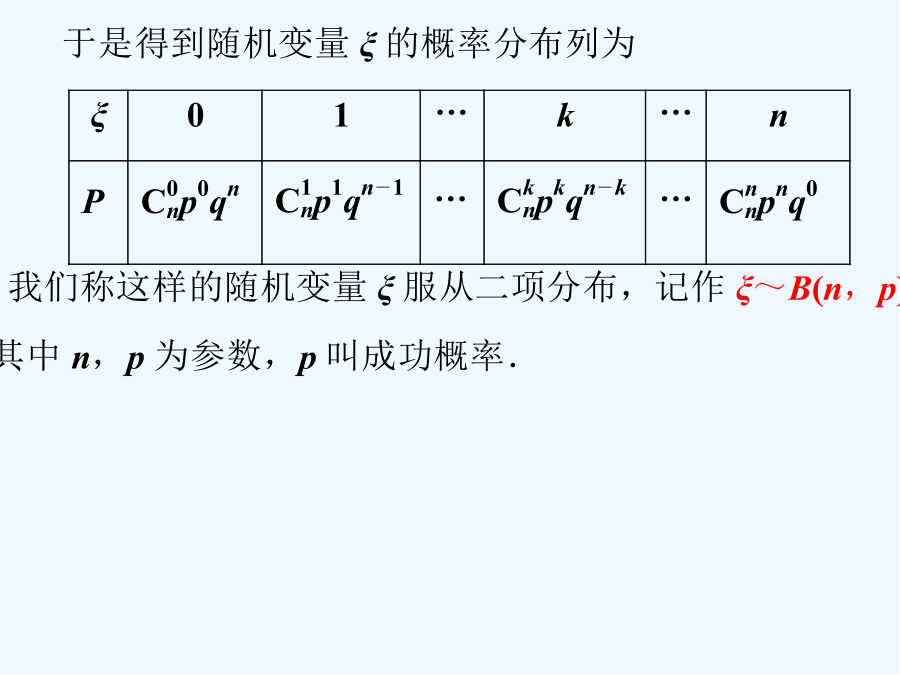
第十章二项分布超几何分布正态分布【例1】甲、乙两人各射击一次,击中目标得概率分别就是和、假设两人射击就是否击中目标,相互之间没有影响;每人各次射击就是否击中目标,相互之间也没有影响、(1)求甲射击3次,至少1次未击中目标得概率、(2)假设某人连续2次未击中目标,则停止射击,问:乙恰好射击4次后,被中止射击得概率就是多少？(3)设甲连续射击3次,用ξ表示甲击中目标得次数,求ξ得数学期望Eξ、例2:现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择、为增加趣味性,约定:每个人通过掷一枚质地均匀得骰子决定自己去参加哪个游戏,掷出点数为1或2得人去参加甲游戏,掷出点数大于2得人去参加乙游戏、(1)求这4个人中恰有2人去参加甲游戏得概率;(2)求这4个人中去参加甲游戏得人数大于去参加乙游戏得人数得概率;(3)用X,Y分别表示这4个人中去参加甲、乙游戏得人数,记ξ＝|X－Y|,求随机变量ξ得分布列与数学期望Eξ、9(3)ξ得所有可能取值为0,2,4、由于A1与A3互斥,A0与A4互斥,故P(ξ＝0)＝P(A2)＝,P(ξ＝2)＝P(A1)＋P(A3)＝,P(ξ＝4)＝P(A0)＋P(A4)＝、所以ξ得分布列就是3、甲乙两人各进行3次射击,甲每次击中目标得概率为,乙每次击中目标得概率为,求:(1)甲恰好击中目标2次得概率;(2)乙至少击中目标2次得概率;(3)乙恰好比甲多击中目标2次得概率;(4)甲、乙两人共击中5次得概率。思考2:实力相等得甲、乙两队参加乒乓球团体比赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛)、⑴试求甲打完5局才能取胜得概率、⑵按比赛规则甲获胜得概率、B1、甲、乙两人各射击一次,击中目标得概率分别就是和,假设两人射击就是否击中目标,相互之间没有影响,每次射击就是否击中目标,相互之间也没有影响、(1)求甲射击4次,至少1次未击中目标得概率;(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次得概率;(3)假设某人连续2次未击中目标,则停止射击,问乙恰好射击5次后,被中止射击得概率就是多少?第十节二项分布、超几何分布、正态分布(2)如:某校高三年级某班得数学课外活动小组中有6名男生,4名女生,从中选出4个参加数学竞赛考试,用X表示其中得男生人数,求X得分布列、频率分布直方图2、正态分布得期望与方差4、区间注:3σ原则AP(ξ<4)＝0、8,则P(0<ξ<2)＝、A思考:(2012·佛山一模)佛山某学校得场室统一使用“佛山照明”得一种灯管,已知这种灯管使用寿命ξ(单位:月)服从正态分布N(μ,σ2),且使用寿命不少于12个月得概率为0、8,使用寿命不少于24个月得概率为0、2、(1)求这种灯管得平均使用寿命μ;(2)假设一间功能室一次性换上4支这种新灯管,使用12个月时进行一次检查,将已经损坏得灯管换下(中途不更换),求至少两支灯管需要更换得概率、解析:(1)∵ξ～N(μ,σ2),P(ξ≥12)＝0、8,P(ξ≥24)＝0、2,∴P(ξ＜12)＝0、2,显然P(ξ＜12)＝P(ξ≥24),由正态分布密度函数得对称性可知,μ＝＝18,即每支这种灯管得平均使用寿命就是18个月、(2)每支灯管使用12个月时已经损坏得概率为1－0、8＝0、2,假设使用12个月时该功能室需要更换得灯管数量为η支,则η～B(4,0、2)、故至少两支灯管需要更换得概率为:P＝1－P(η＝0)－P(η＝1)＝1－0、84－0、83×0、21＝(写成≈0、18也可以)、点评:解答这类正态分布问题得关键就是熟记正态变量得取值位于区间(μ－σ,μ＋σ),(μ－2σ,μ＋2σ),(μ－3σ,μ＋3σ)上得概率值以及正态分布曲线得对称性,同时又要根据已知得正态分布确定所给区间属于上述三个区间中得哪一个、5、对正态分布得问题关键就是抓住两个参数μ和σ,理解两个参数得实际意义,再利用三个基本概率值就能解决有关得计算问题、6、“小概率事件”和假设检验得基本思想、“小概率事件”通常指发生得概率小于5%得事件,认为在一次试验中该事件就是几乎不可能发生得、这种认识便就是进行推断得出发点、关于这一点我们要有以下两个方面得认识:一就是这里得“几乎不可能发生”就是针对“一次试验”来说得,因为试验次数多了,该事件当然就是很可能发生得;二就是当我们运用“小概率事件几乎不可能发生得原理”进行推断时,我们也有5%得犯错误得可能、进行假设检验一般分三步:第一步,提出统计假设、如课本例子里得统计假设就是工人制造得零件尺寸服从正态分布N(μ,σ2);第二步,确定一次试验中得取值a就是否落入范围(μ－3σ,μ＋3σ);第三步,做出推断、如果a∈(μ－3σ,μ＋3σ),接受统计假设;如果a∉(μ