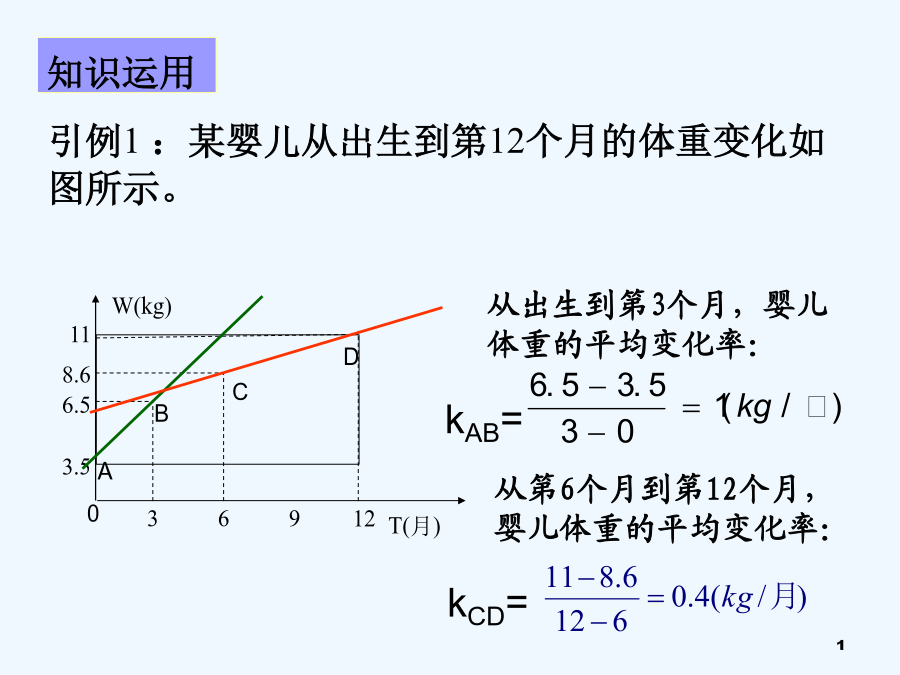
T(月)T(月)课堂小结平均变化率已知函数，分别计算下列区间上的平均变化率：在高台跳水运动中,运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系在高台跳水运动中,运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系探究：2、在某一时刻的瞬时速度怎样表示？大家有疑问的，可以询问和交流大家有疑问的，可以询问和交流一般地，函数y=f(x)在x=x0处的瞬时变化率是由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:例、将原油精炼为汽油、柴油、塑胶等各种不同产品，需要对原油进行冷却和加热。如果第xh时，原油的温度(单位：℃)为f(x)=x2-7x+15(0x8h).计算第2h和第6h时，原油温度的瞬进变化率，并说明它们的意义。所以，f'(6)=5说明在第6h附近，原油温度大约以5℃/h的速度上升；注意：1,函数f(x)=x2在点(2,4)处的切线的斜率为()A.f(2)B.f(4)C.f’(2)D.f’(4)2.如图,试描述函数f(x)在x=-5,-4,-2,0,1附近的变化情况:3.根据下列条件，分别画出函数图象在这点附近的大致形状:(1)f(1)=-5,f’(1)=-1(2)f(5)=10,f’(5)=15(3)f(10)=20,f’(10)=04.如右图所示，向高为10cm的杯子等速注水，3分钟注满。若水深h是关于注水时间t的函数，则下面两个图象哪一个可以表示上述函数？例2.请分别计算出下面两个图象表示的函数h(t)在区间[0，3]上的平均变化率。谢谢