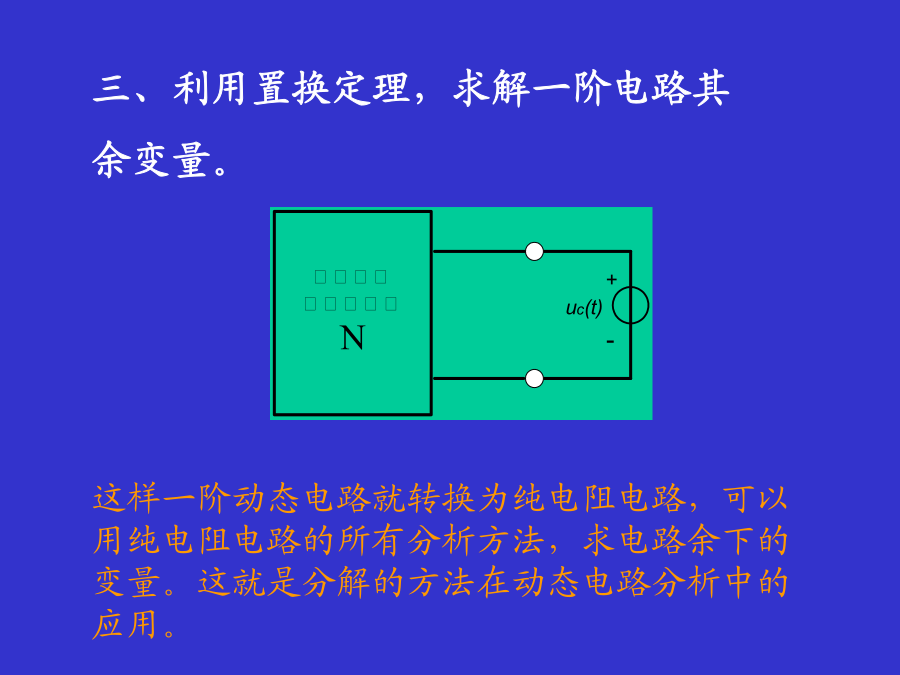
第七章一阶电路引言二、如何分析一阶电路？7-1分解的方法在动态电路分析中的应用二、RC电路的分析2、一阶微分方程的求解：特解的形式：3、RC电路微分方程的求解三、利用置换定理，求解一阶电路其余变量。四、小结73一阶电路的零输入响应建立图(b)电路的一阶微分方程最后得到电路的零输入响应为:U0换路：电路由电源接入或断开，元件参数或电路结构突然改变。二、RL电路的零输入响应列出KCL方程，得到微分方程三、结论：例1：电路如图(a)所示，已知电容电压uC(0-)=6V。t=0闭合开关，求t>0时uC(t)、iC(t)、iR(t)。电阻中的电流iR(t)可以用与iC(t)同样数值的电流源代替电容，用电阻并联的分流公式求得iR(t)例2：例3：74一阶电路的零状态响应+1）uC(t)的零状态响应是从零按指数规律上升到它的稳态值uC();4、求电容电流：二、RL电路的零状态响应R1）iL的零状态响应是从零按指数规律上升到它的稳态值iL()。当t＝4，iL（t）接近稳态值。iL()=IS,是电感短路时的值。解一：三、结论：例1电路如图(a)，已知uC(0-)=0。t=0打开开关，求：t0的uC(t)，iC(t)及电阻电流i1(t)。当电路达到新的稳定状态时，电容相当开路得例2电路如图(a)所示，已知电感电流iL(0-)=0。t=0闭合开关，求：t0的iL(t)，uL(t)，i(t)。75线性动态电路的叠加定理以电容电压uC(t)为变量，列出图(b)电路微分方程于是得到电容电压表达式：①固有响应：与输入无关，由电路本身决定。线性动态电路中任一支路电压或电流的完全响应等于零输入响应与零状态响应之和。三、完全响应的三种分解方式：四、线性动态电路叠加定理与线性电阻电路叠加定理的关系例1下图所示电路原来处于稳定状态。t=0时开关断开，求t0的电感电流iL(t)和电感电压uL(t)。解：在t<0时，电阻R1被开关短路，电感电流的初始值为式中其中第一项是瞬态响应，第二项是稳态响应。电路在开关断开后，经过(4～5)的时间，即经过(8～10)ms的过渡时期，就达到了稳态。电感电流iL(t)的全响应也可以用分别计算出零输入响应和零状态响应，然后相加的方法求得。电感电流iL(t)的零输入响应为iL(t)的全响应为零输入响应与零状态响应之和例2电路如下图(a)所示。已知uC(0-)=4V，uS(t)=(2+e-2t)V，求电容电压uC(t)的全响应。解：将全响应分解为(零输入响应)＋(2V电压源引起的零状态响应)＋(e-2t电压源引起的零状态响应)。现在分别计算响应的几个分量然后相加得到全响应。1.求电路的零输入响应[见图(b)电路]2.求2V电压源引起的零状态响应[见图(c)电路]3.求2e-2tV电压源引起的零状态响应[见图(d)电路]由此求得4.最后求得全响应如下76三要素法当动态元件为电感时，典型一阶电路如(b)，其完全响应如右式。可见电感电流的完全响应也取决于三个要素：初值iL(0)，终值iL()和时间常数。二、三要素法：三、三个要素的求法2.求稳态值x()10V2.再求i1(0+),i2(0+)：例2例3图(a)所示电路处于稳定状态。t=0时开关闭合，求：t0的电容电压uC(t)和电流i(t)，并画波形图。4.代入三要素一般表达式也可以用叠加定理分别计算2A电流源，10V电压源和电容电压uC(t)单独作用引起响应之和由于电路中每个响应具有相同的时间常数，不必重新计算，用三要素公式得到例4：图示电路中，开关转换前电路已处于稳态，t=0时开关S由1端接至2端，求：t>0时的电感电流iL(t)，电阻电流i2(t)，i3(t)和电感电压uL(t)。4.计算iL(t)，uL(t)，i2(t)和i3(t)。例5：图(a)所示电路，在t=0时闭合开关，求：电容电压uC(t)和电流i2(t)的零状态响应。时间常数为本小节讨论的直流一阶电路中包含有在不同时刻转换的开关，在开关没有转换的时间间隔内，它是一个直流一阶电路，可以用三要素法来计算。对于这一类电路，我们可以按照开关转换的先后次序，从时间上分成几个区间，分别用三要素法来求解电路的响应。这就是所谓的子区间分析法。例1下图（a）所示电路中，电感电流iL(0-)=0,t=0时，开关S1闭合，经过0.1s，再闭合开关S2，同时断开S1。试求电感电流iL(t)，并画波形图。解：1.在0t0.1s时间范围内响应的计算S1闭合后，iL(0+)=iL(0-)=0，处于零状态，电感电流为零状态响应。可以用三要素法求解2.在t0.1s时间范围内响应的计算根据三要素公式（8－25）得到电感电流iL(t)的波形曲线如图(b)所示。在t=0时，它从零开始，以时间常数1=0.1s确定的