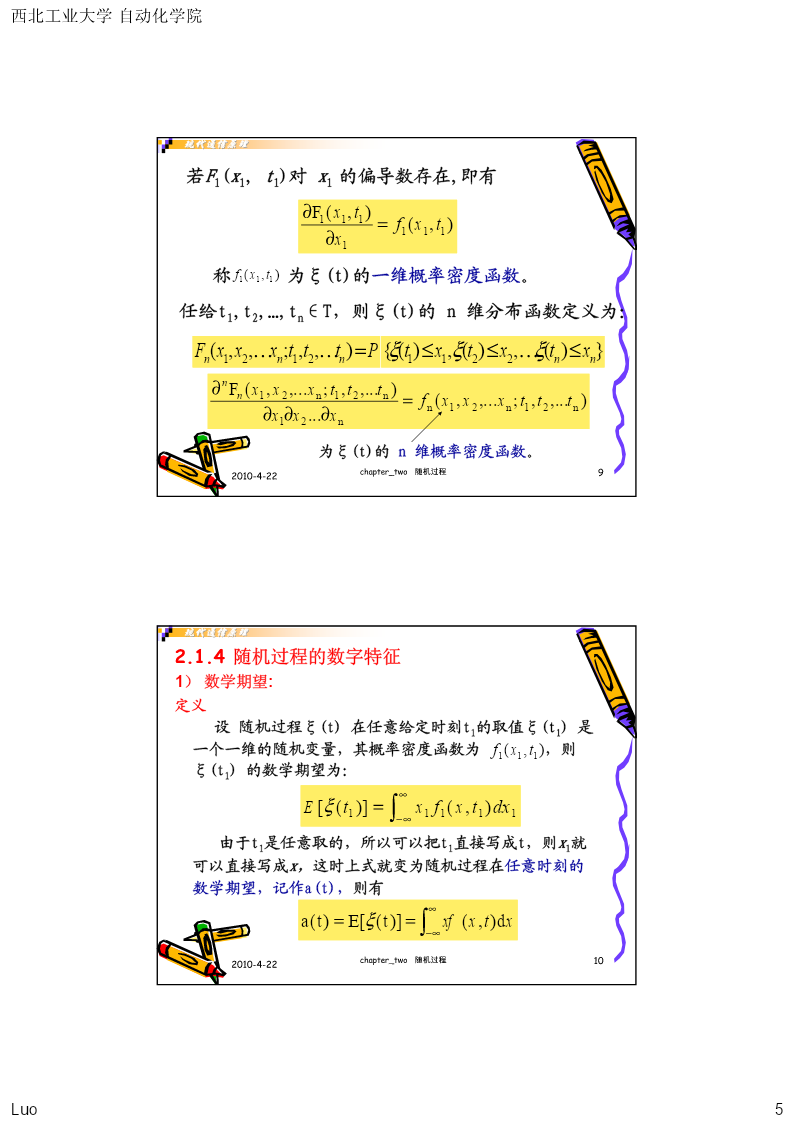
西北工业大学自动化学院现代通信原理现代通信原理西北工业大学自动化学院现代通信原理第二章随机过程•2.1随机过程的基本概念和统计特性•2.2平稳随机过程•2.3高斯随机过程•2.4随机过程通过线性系统•2.5窄带随机过程•2.6正弦波加窄带高斯噪声返回课程目录随机过程2010-4-22chapter_two2Luo1西北工业大学自动化学院现代通信原理2.1随机过程的基本概念和统计特性•2.1.1随机过程的一般表述•2.1.2随机过程的定义•2.1.3随机过程的统计特性•2.1.4随机过程的数字特征随机过程2010-4-22chapter_two3现代通信原理2.1.1随机过程的一般表述自然界中事物的变化过程大致分为两类:•确定性过程–其变化过程具有确定的形式，或者说具有必然的变化规律。–用数学语言来说，其变化过程可以用一个或几个时间t的确定函数来描述。•随机过程–没有确定的变化形式，也就是说，每次对它的测量结果没有一个确定的变化规律。–用数学语言来说，这类事物变化的过程不可能用一个或几个时间t的确定函数来描述。–随机信号和噪声统称为随机过程。随机过程2010-4-22chapter_two4Luo2西北工业大学自动化学院现代通信原理2.1.2随机过程的定义:一般定义：随机过程是指依赖于时间参量t变化的随机变量的总体或集合；也可以叫做样本函数的总体或集合。习惯用ξ(t)表示。严格定义：设Sk(k=1,2,…)是随机试验。每一次试验都有一条时间波形（称为样本函数或实现），记作xi(t)，所有可能出现的结果的总体{x1(t),x2(t)，…,xn(t)，…}就构成一随机过程，记作ξ(t)。z无穷多个样本函数的总体叫做随机过程。示意图随机过程2010-4-22chapter_two5现代通信原理图2-1样本函数的总体随机过程2010-4-22chapter_two6Luo3西北工业大学自动化学院现代通信原理z随机过程的两个基本特征：¾时间函数¾随机变量•在进行观测前是无法预知是空间中哪一个样本；•全体样本在t1时刻的取值ξ(t1)是一个不含t变化的随机变量；•随机过程是由全部实现构成的整体，每个实现都是确定的时间函数，而随机性就体现在出现哪一个实现是不确定的。随机过程2010-4-22chapter_two7现代通信原理2.1.3随机过程的统计特性•设ξ(t)表示一个随机过程，在任意给定的时刻t1∈T，其取值ξ(t1)是一个一维随机变量。•随机变量的统计特性可以用分布函数或概率密度函数来描述。•我们把随机变量ξ(t1)小于或等于某一数值x1的概率，简记为F1(x1,t1)，即Pt{()ξ11≤x}F111(,)xt=≤P{ξ()t1x1}称F1(x1,t1)为随机过程ξ(t)的一维分布函数。随机过程2010-4-22chapter_two8Luo4西北工业大学自动化学院现代通信原理若F1(x1,t1)对x1的偏导数存在,即有∂F1(x1,t1)=f1(x1,t1)∂x1称f1(x1,t1)为ξ(t)的一维概率密度函数。任给t1,t2,…,tn∈T，则ξ(t)的n维分布函数定义为：Fxxnnn(,12,……xtt;,,12t)=P{()ξtxtx1122≤≤,ξξ(),…(txnn)≤}n∂Fn(x1,x2,...xn;t1,t2,...tn)=fn(x1,x2,...xn;t1,t2,...tn)∂x1∂x2...∂xn为ξ(t)的n维概率密度函数。随机过程2010-4-22chapter_two9现代通信原理2.1.4随机过程的数字特征1）数学期望:定义设随机过程ξ(t)在任意给定时刻t1的取值ξ(t1)是一个一维的随机变量，其概率密度函数为f1(x1,t1)，则ξ(t1)的数学期望为：∞E[ξ(t1)]=x1f1(x,t1)dx1∫−∞由于t1是任意取的，所以可以把t1直接写成t，则x1就可以直接写成x，这时上式就变为随机过程在任意时刻的数学期望，记作a(t)，则有∞a(t)=E[ξ(t)]=xf(x,t)dx∫−∞随机过程2010-4-22chapter_two10Luo5西北工业大学自动化学院现代通信原理含义1、随机过程的数学期望表示随机过程的n个样本函数曲线的摆动中心，即均值。2、随机过程的数学期望被认为是时间t的函