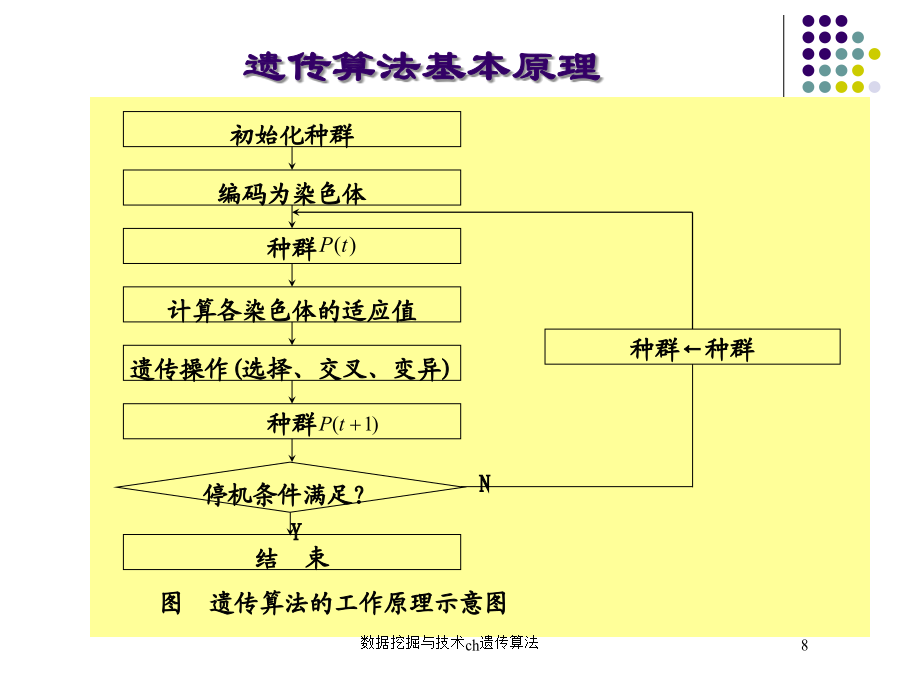
数据挖掘与技术ch遗传算法生物进化理论和遗传学的基本知识生物进化理论和遗传学的基本知识生物进化理论和遗传学的基本知识生物进化理论和遗传学的基本知识生物进化理论和遗传学的基本知识遗传算法可定义为一个8元组：GA=(C,E,P0,M,,,,T)式中，C—个体的编码方法；E—个体适应值评价函数；P0—初始种群；M—群体大小；—选择算子；—交叉算子；—变异算子；T—遗传算法终止条件。初始化种群遗传算法的关键技术包括：编码问题；初始种群的产生；确定适应值函数；选择遗传操作算子；停机条件。编码问题由于遗传算法不能直接处理解空间的解数据，因此必须通过编码将它们表示成遗传空间的基因型串结构数据。编码方法在很大程度上决定了如何进行群体的遗传进化运算以及遗传进化的效率。由于不同的编码方法具有不同的特点，为了提高遗传算法的效率，应根据不同的情况采用不同的编码方式。主要的编码方法有二进制编码、浮点数编码、符号编码、多参数编码、可变长染色体编码等。编码问题在遗传算法中一般用二值（0，1）向量表示染色体，故先要对规则进行编码。编码采用二进制，将由特征和类别组成的训练例子集编码成二进制字符串的遗传样本。一个样本Mi是一个二元组，其形式如下：Mi=[xi，yi]，其中：i为样本号；x为条件部分，即训练例子的各特征编码；y为结论部分，即训练例子的类别。具体的编码规则如下：若属性为范畴型，定义属性段的宽度等于属性取值个数。对于每个属性段，若第一位为‘*’，表示该属性取值可以为任意；否则，各位若取值为1，表示取该属性值，0表示不取该属性值。例如，某条件属性Ci对应的编码二进制串为011001，表示该属性取第二个属性值或第三个属性值或第六个属性值，即若属性为数值型，定义属性段的宽度，其中n为该属性的取值个数。对于每个属性段，若第一位为‘*’，表示该属性取值可以为任意初始种群的产生GA以初始种群作为初始点开始迭代。初始种群大小表示群体中所含个体的数量。当个体数量取值较小时，可提高遗传算法的运算速度，但搜索空间分布范围有限，降低了群体的多样性，有可能会引起遗传算法的早熟现象；当个体数量取值较大时，一方面计算复杂，会使遗传算法的运行效率降低，另一方面，部分高适应值的个体可能被淘汰，影响交叉。初始种群的一般取值范围是20~100。产生初始种群的方法通常有两种：（1）对问题的解无任何先验知识的情况，采用随机产生样本的方法；（2）对于具有某些先验知识的情况，可首先将这些先验知识转变为必须满足的一组要求，然后在满足这些要求的解中随机地选取样本。这样选择初始种群可使遗传算法更快地达到最优解。遗传算法关键技术遗传算法关键技术选择遗传操作算子遗传算法关键技术遗传算法关键技术遗传算法关键技术遗传算法关键技术遗传算法关键技术遗传算法关键技术遗传算法关键技术遗传算法关键技术遗传算法关键技术遗传算法关键技术遗传算法的步骤遗传算法的实例4）选择率和期望值选择率：平均适应值：期望值：5）实选值期望值取整数。如下表：表1：初始种群参数计算表2：初始种群的遗传过程表3：新种群参数计算表4：新种群的遗传过程遗传算法在适应度函数选择不当的情况下有可能收敛于局部最优，而不能达到全局最优。对于动态数据，用遗传算法求最优解比较困难，因为染色体种群很可能过早地收敛，而对以后变化了的数据不再产生变化。为防止过早的收敛，研究者提出了一些方法增加基因的多样性。其中一种是所谓触发式超级突变，就是当染色体群体的质量下降（彼此的区别减少）时增加变异概率；另一种叫随机外来染色体，是偶尔加入一些全新的随机生成的染色体个体，从而增加染色体多样性。选择过程很重要，但交叉和变异的重要性存在争议。一种观点认为交叉比变异更重要，因为变异仅仅是保证不丢失某些可能的解；而另一种观点则认为交叉过程的作用只不过是在种群中推广变异过程所造成的更新，对于初期的种群来说，交叉几乎等效于一个非常大的变异率，而这么大的变异很可能影响进化过程。遗传算法很快就能找到良好的解，即使是在很复杂的解空间中。遗传算法并不一定总是最好的优化策略，优化问题要具体情况具体分析。所以在使用遗传算法的同时，也可以尝试其他算法，互相补充，甚至根本不用遗传算法。遗传算法不能解决那些“大海捞针”的问题，所谓“大海捞针”问题就是没有一个确切的适应度函数表征个体好坏的问题，遗传算法对这类问题无法找到收敛的路。对于任何一个具体的优化问题，调节遗传算法的参数可能会有利于更好的更快的收敛，这些参数包括个体数目、交叉律和变异律。例如太大的变异律会导致丢失最优解，而过小的变异律会导致算法过早的收敛于局部最优点。对于这些参数的选择，现在还没有实用的上下限。适应度函数对