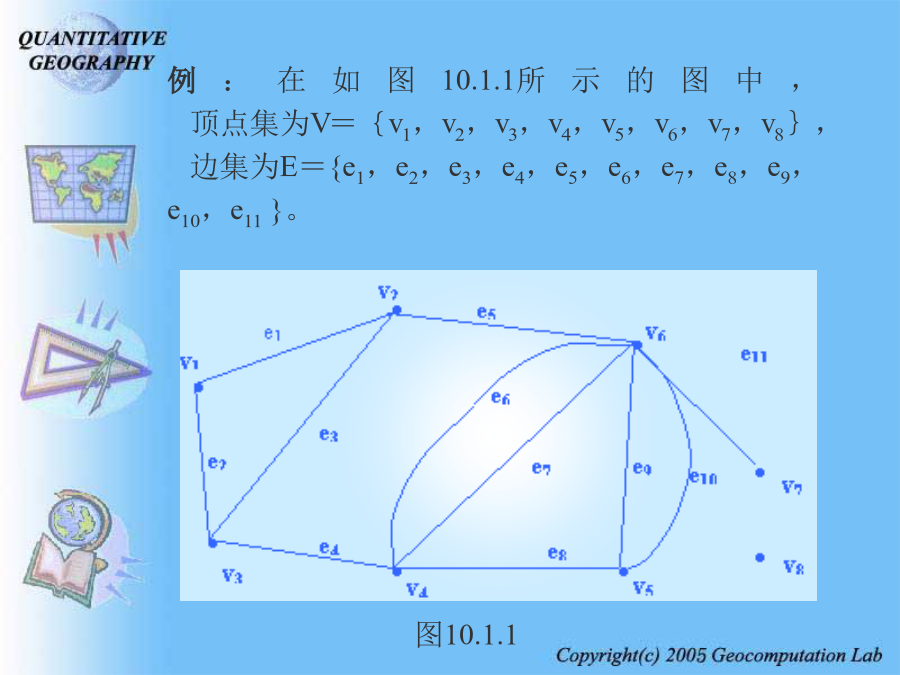
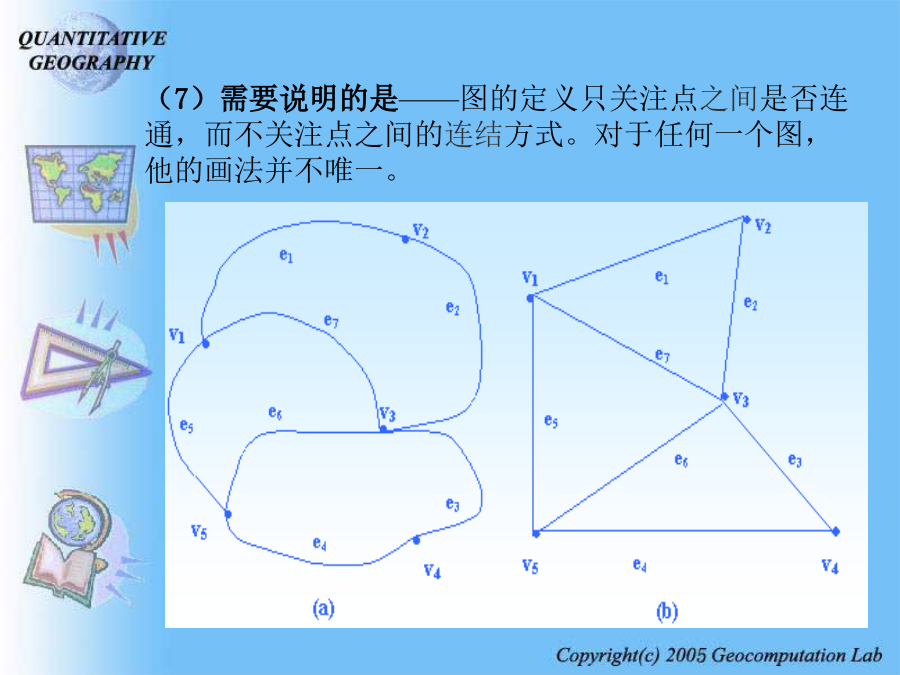
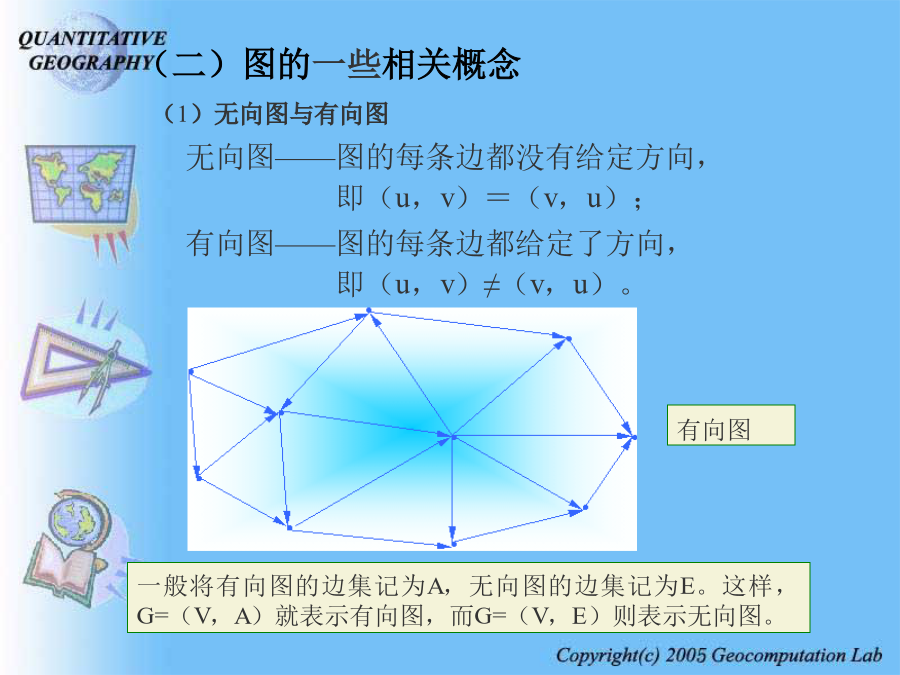
对于许多现实的地理问题，譬如，城镇体系问题，城市地域结构问题，交通问题，商业网点布局问题，物流问题，管道运输问题，供电与通讯线路问题，…，等等，都可以运用网络分析方法进行研究。本章主要内容：第一节地理网络的图论描述（1）图：设V是一个由n个点vi(i=1，2，…，n)所组成的集合，即V={v1，v2，…，vn}，E是一个由m条线ei（i=1，2，…，m）所组成的集合，即E={e1，e2，…，em}，而且E中任意一条线，都是以V中的点为端点；任意两条线除了端点外没有其它的公共点。（3）边：E中每一条线称为图G的边（或弧）；若一条边e连接u，v两个顶点，则记为e＝（u，v）。例：在如图10.1.1所示的图中，顶点集为V＝｛v1，v2，v3，v4，v5，v6，v7，v8｝，边集为E＝{e1，e2，e3，e4，e5，e6，e7，e8，e9，e10，e11}。（6）在现实地理系统中，对于地理位置、地理实体、地理区域以及它们之间的相互联系，可以经过一定的简化与抽象，将它们描述为图论意义下的地理网络，即图。列昂纳德·欧拉——七桥问题（7）需要说明的是——图的定义只关注点之间是否连通，而不关注点之间的连结方式。对于任何一个图，他的画法并不唯一。（二）图的一些相关概念（2）赋权图。如果图G＝（V，E）中的每一条边（vi，vj）都相应地赋有一个数值wij，则称G为赋权图，其中wij称为边（vi，vj）的权值。除了可以给图的边赋权外，也可以给图的顶点赋权。这就是说，对于图G中的每一顶点vj，也可以赋予一个载荷a(vj)。（3）关联边。若e＝（u，v），则称u和v是边e的端点，e是u和v的关联边。（4）环。若e的两个端点相同，即u＝v，则称为环。（5）多重边。若连接两个端点的边多于一条以上，则称为多重边。（8）点与次。以点v为端点的边的个数称为点v的次，记为d(v)。次等于1的点称为悬挂点；与悬挂点关联的边称为悬挂边；次为零的点称为孤立点。次为奇数的点称为奇点；次为偶数的点称为偶点。（9）连通图。在图G中，若任何两点之间至少存在一条路（对于有向图，则不考虑边的方向），则称G为连通图，否则称为不连通图。（10）路（链）。若图G＝（V，E）中，若顶点与边交替出现的序列（对于有向图来说，要求排在每一条边之前和之后的顶点分别是这条边的起点和终点）：P＝{vi1，ei1，vi2，ei2，…，eik-1，vik}满足eit=(vit，vi，t+1)(t=1,2,…,k-1)则称P为一条从vi1到vik的路（或链），简记为P＝{vi1，vi2，…，vik}。（11）回路。若一条路的起点与终点相同，即vi1=vik，则称它为回路。（12）树。不含回路的连通的无向图称为树。（13）基础图。从一个有向图D＝（V，A）中去掉所有边上的箭头所得到的无向图，就称为D的基础图，记之为G（D）。（14）截。如果从图中移去边的一个集合将增加亚图的数目时，被移去的边的集合就称为截。（15）子图。设G＝（V，E）是一个无向图，V1与E1分别是V与E的子集，即V1V，E1E。如果对于任意ei∈E1，其两个端点都属于V1，则称G1＝（V1，E1）是图G的一个子图。（16）支撑子图。设G1＝（V1，E1）是图G＝（V，E）的一个子图，如果V1＝V，则称G1是G的支撑子图。（17）支撑树。设G＝（V，E）是一个无向图，如果T＝（V1，E1）是G的支撑子图，并且T是树，则称T是G的一个支撑树。（18）树的重量。一个树的所有边的权值之和称为该树的重量。（19）最小支撑树。在一个图的所有支撑树中，重量最小的那个叫做该图的最小支撑树。二、地理网络的测度目前关于地理网络的拓扑研究，最多、最常见的是基于平面图描述的二维平面网络。所谓平面图，被规定为：各连线之间不能交叉，而且每一条连线除顶点以外，不能再有其它的公共点（牛文元，1987）。以下的讨论，除非特别申明外，都限于二维平面网络。（一）关联矩阵与邻接矩阵v3邻接矩阵——测度网络图中各顶点之间的连通性程度。假设图G＝（V，E）的顶点集为V={v1，v2，…，vn}，则邻接矩阵是一个n阶方阵，可表示为：该图的邻接矩阵为：（二）有关测度指标◣β指数——线点率，是网络内每一个节点的平均连线数目。◣β=0，表示无网络存在；网络的复杂性增加，则β值也增大。◣没有孤立点存在的网络，连线数目为n-p,则β指数为(2)回路数k◣回路是一种闭合路径,它的始点同时也是终点。◣若网络内存在回路，则连线的数目就必须超过n-p（最低限度连接网络的连接数目）。◣回路数k——实际连线数目减去最低限度连接的连线数目，即(3)指数◣指数——实际回路数与网络内可能存在的最大回路数之间的比率。◣网络内可能存在的