如果您无法下载资料,请参考说明:
1、部分资料下载需要金币,请确保您的账户上有足够的金币
2、已购买过的文档,再次下载不重复扣费
3、资料包下载后请先用软件解压,在使用对应软件打开
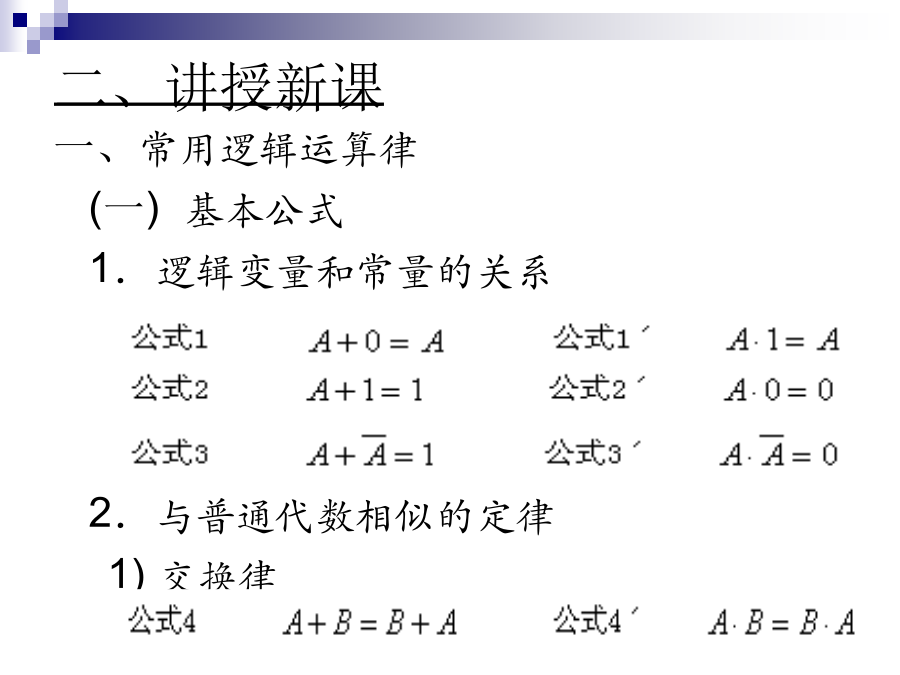
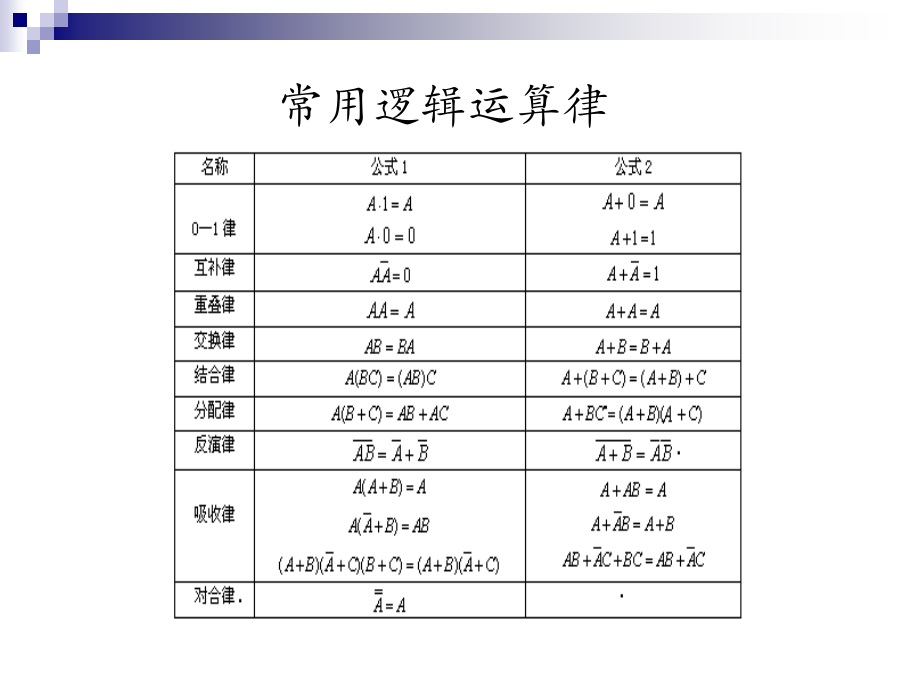
一、引入新课一、常用逻辑运算律(一)基本公式1.逻辑变量和常量的关系2.与普通代数相似的定律1)交换律2)反演律(摩根定律)摩根定律可推广到多个变量。3)还原律(对合律或非非律或否定律)4)吸收律公式13可推广并表述为:若一个逻辑式中有三个与项,其中一个含有原变量,另一个含有反变量,如果这两个与项的其余因子都是第三个与项中的因子,则第三个与项是冗余项,可以消去。常用逻辑运算律二、逻辑式的化简与变换(代数法)(一)化简与变换的意义对逻辑式进行化简和变换,可以得到最简的逻辑式和所需要的形式,设计出最简洁的逻辑电路。1.逻辑式的五种表达式除了与或表达式外还有或与表达式、与非—与非表达式、或非—或非表达式、与或非表达式等。思考:请大家使用逻辑代数的基本公式和定律验证一下上述五个公式是否相等?2.逻辑式的逻辑电路图3.化简的意义和最简的概念同一个函数可以有不同的表达式,即使对于某一类表达式而言,其表达式也不是唯一的,有的较复杂的,有的较简单,相应的逻辑电路也较复杂或较简单。最简的与或表达式的条件是:在不改变逻辑关系的情况下,首先乘积项(与项)的个数最少;在此前提下,其次是每一个乘积项中变量的个数最少。化简与或表达式的方法有两种:代数法和图解法。(4)配项法解:解:解法1:练习题四、课堂小结五、作业