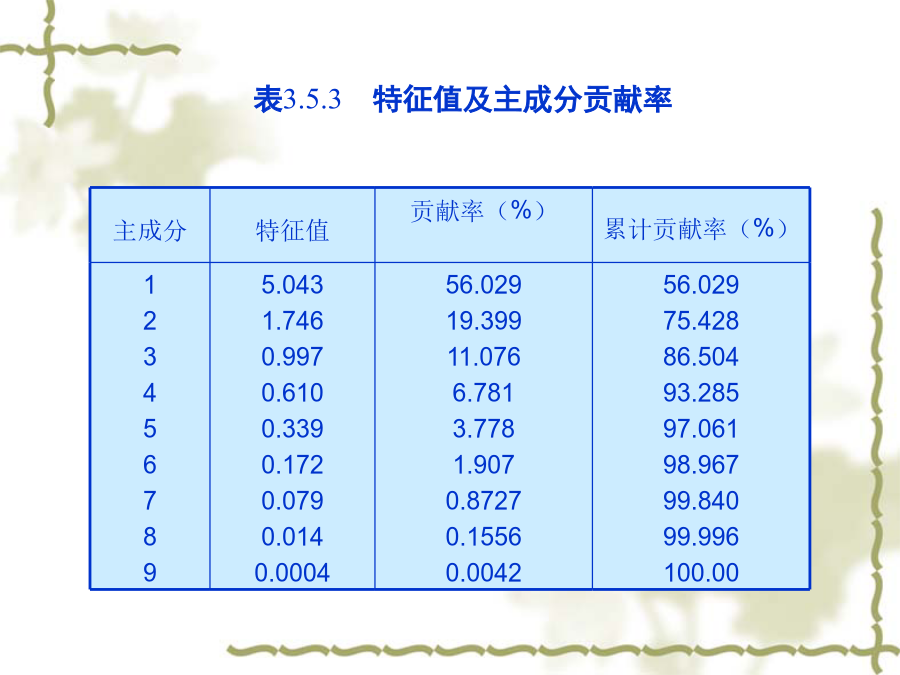
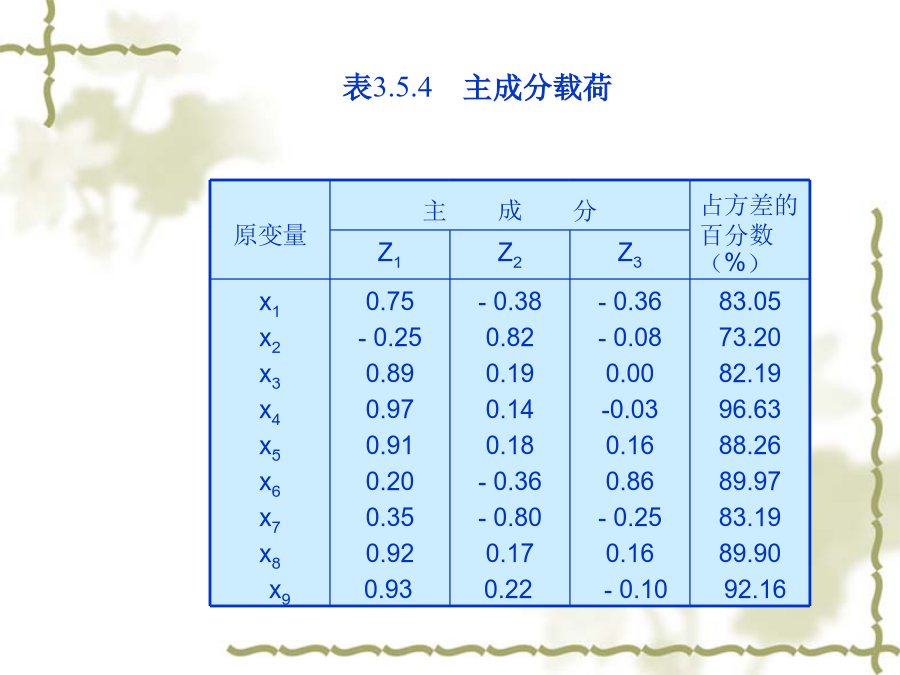
§3.5主成分分析方法基本原理z1，z2，…，zm分别称为原变量指标x1，x2，…，xP的第一，第二，…，第m主成分。主成分分析的主要任务就是确定每一个主成分Zi在原变量xj上的载荷lij系数lij的确定原则：①zi与zj（i≠j；i，j=1，2，…，m）相互无关；②z1是x1，x2，…，xP的一切线性组合中方差最大者，z2是与z1不相关的x1，x2，…，xP的所有线性组合中方差最大者；……；zm是与z1，z2，……，zm－1都不相关的x1，x2，…，xP的所有线性组合中方差最大者。计算步骤3.主成分分析方法应用实例计算过程：①对原始数据作标准化处理，代入公式（3.5.4）计算，得到相关系数矩阵（表3.5.2）。②由相关系数矩阵计算特征值、各个主成分的贡献率、累计贡献率（表3.5.3）。由表3.5.3可知，第一，第二，第三主成分的累计贡献率已高达86.5%，故只需求出第一、第二、第三主成分z1，z2，z3即可。③对于特征值=5.043，=1.746，=0.997分别求出其特征向量e1，e2，e3，再用公式（3.5.5）计算各变量x1，x2，…，x9在主成分z1，z2，z3上的载荷（表3.5.4）。表3.5.2相关系数矩阵表3.5.3特征值及主成分贡献率表3.5.4主成分载荷分析：①第一主成分z1与x1，x3，x4，x5，x8，x9有较大的正相关，可看作是流域盆地规模的代表；②第二主成分z2与x2有较大的正相关，与x7有较大的负相关，可看作是流域侵蚀状况的代表；③第三主成分z3与x6有较大的正相关，可看作是河系形态的代表。④该流域系统的9项要素可以被归纳为三类：流域盆地的规模、流域侵蚀状况、流域河系形态。选取其中相关系数绝对值最大者作为代表，则流域面积、流域盆地出口的海拔高度和分叉率可作为这三类要素的代表，利用这三个要素代替原来九个要素进行系统分析，可以使问题大大地简化。（2）实例之二：中国大陆31个省（市、区）第三产业综合发展水平的主成分分析与评估吴玉鸣（2000）运用主成分分析法对中国大陆31个省（市、区）第三产业综合发展水平进行了定量评价研究，其评价过程与结果为：①选取表3.4.5中的7项指标构成综合评价指标体系，首先对原始数据做标准化处理，然后计算各指标之间的相关系数矩阵，结果如表3.5.5所示。②计算出相关矩阵的特征值，以及各主成分的贡献率和累计贡献率，结果如表3.5.6所示。③计算主成分载荷，结果见表3.5.7。④计算各省（市、区）在第一、二、三主成分上的得分，结果见表3.5.8。表3.5.5相关系数矩阵表3.5.6特征值及主成分贡献率和累计贡献率表3.5.8中国各省（市、区）第三产业发展水平的主成分得分评价：①第一主成分得分排在前三位的是上海、北京、天津，其分值依次为3.25739、3.05536、1.69569；得分较高的有辽宁、广东、福建，其分值依次为0.66343、0.46952、0.26928。②第二主成分得分排在前三位的是浙江、黑龙江、山西，其分值依次为1.4885、1.42711、1.14035；得分较高的有江苏、上海、广东、河北、湖北、河南、山东、安徽、云南、辽宁、天津，其分值依次为0.91157、0.87823、0.85841、0.78499、0.64049、0.63492、0.61723、0.50127、0.46638、0.44153、0.41810。③第三主成分得分排在前三位的是湖南、云南、江西，其分值依次为1.88480、1.69846、1.52608，得分较高的有广西、海南、北京、广东、浙江、四川、重庆，其分值依次为1.14659、1.13406、0.88652、0.75405、0.63373、0.57190、0.50662。④综合主成分得分在全国平均水平之上（>0）的，依次为上海、北京、天津、广东、辽宁、浙江、江苏、黑龙江、福建，它们是第三产业综合发展水平较发达的区域，其中，上海、北京、天津三个直辖市得分最高（均在0.85以上）；其它省（市、区）则位于全国平均水平之下（<0）；得分居于最后两位的是贵州和西藏两省区（<-0.70），其第三产业综合发展水平最低。