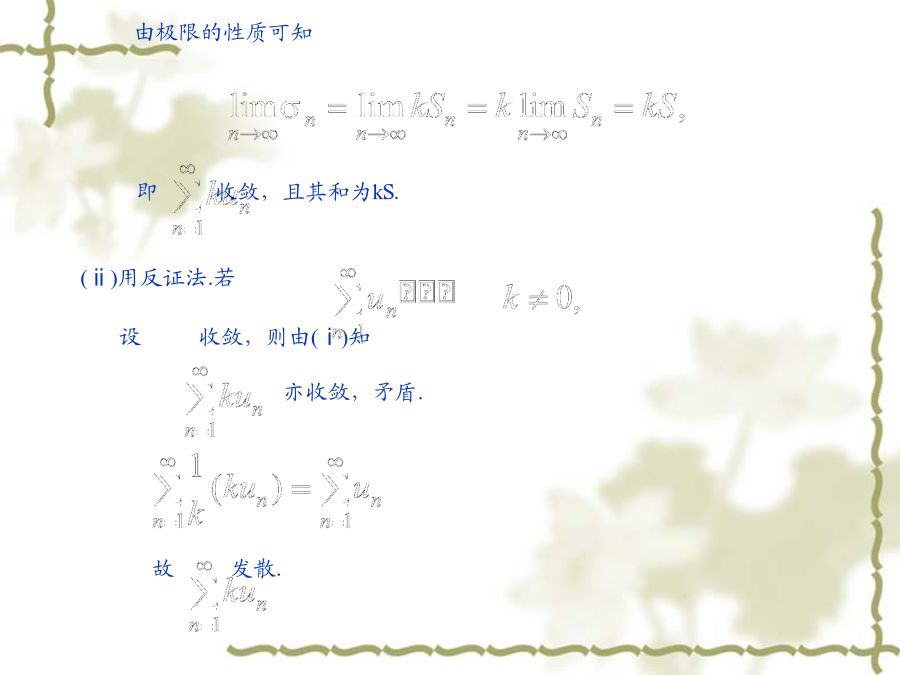
一、无穷级数的概念定义2称为级数的前n项和(n=1,2,···).简称部分和.定义3若收敛，则称若中至少有一项为(非常数)函数，则称为函数项级数.特别如果，则称为幂级数.例1试判定级数的收敛性.例2判定级数的收敛性.当|r|>1时，，因而，即级数发散.例3判定级数的收敛性.二、级数的基本性质由极限的性质可知例4判定级数的收敛性.性质2若收敛，其和为S；收敛，其和为，则必收敛，其和为.例5判定的收敛性.性质3在中去掉或添加有限项，所得新级数与原来级数的收敛性相同.例6判定的收敛性.性质4收敛级数添括号后所得新级数仍收敛，且其和不变.注意收敛级数去括号所得到的新级数不一定为收敛级数.例如(1–1)+(1–1)+···+(1–1)+···收敛于0，但是去括号后可得新级数为发散级数.(1)若收敛，发散，则必定发散.性质5(级数收敛的必要条件)若收敛，则必有例7判定级数的收敛.可见，即添号以后的级散发散.因此原级数亦发散.因为如果原级数收敛，由性质4知，添号以后级数亦必收敛，从而矛盾.利用级数收敛的必要条件及反证法可以得知：例8判定级数的收敛性.例9选择题