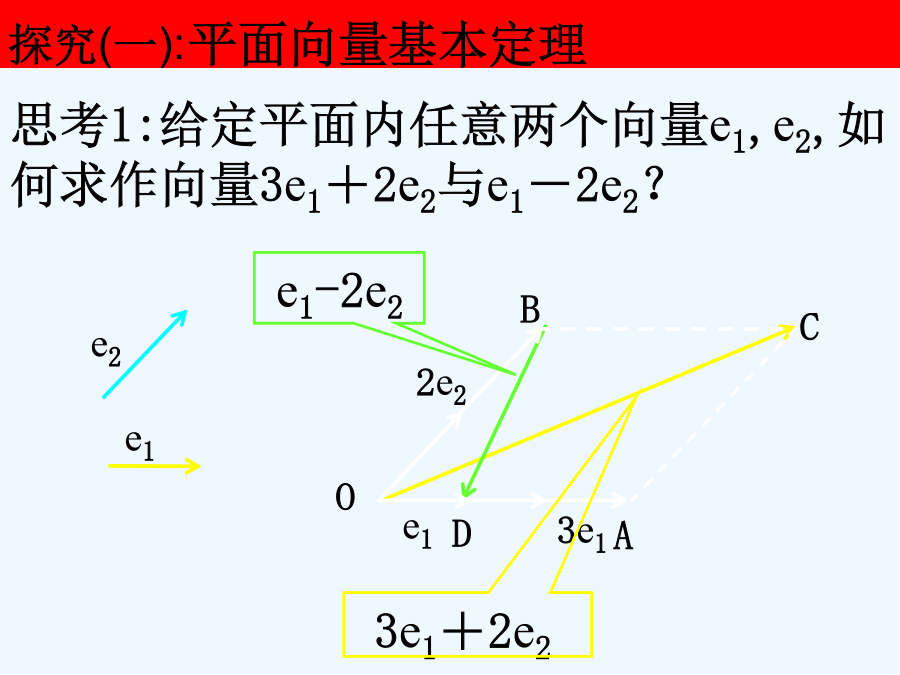
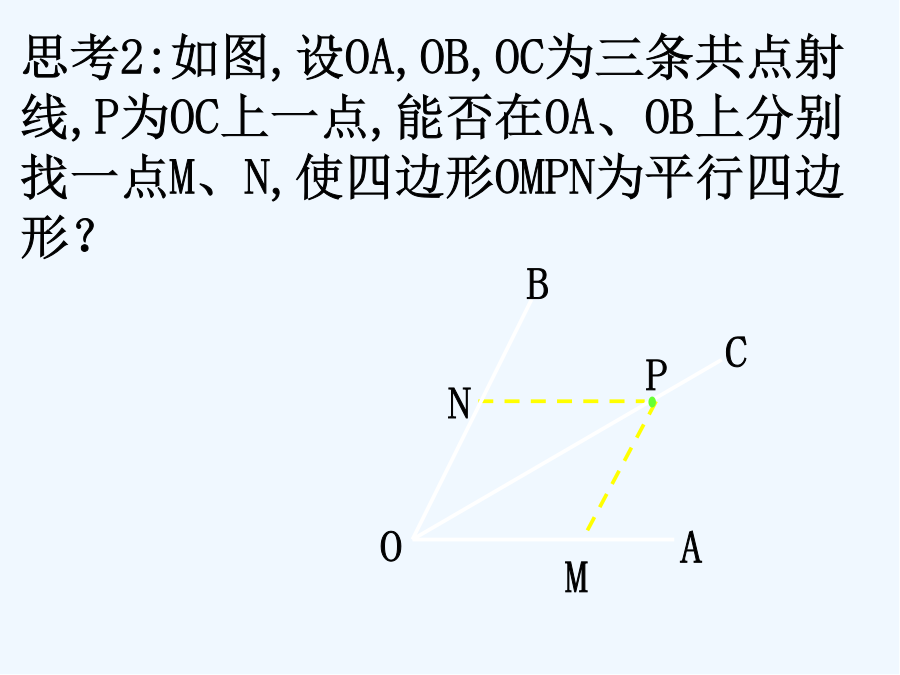
平面向量的基本定理及坐标表示问题提出3、平面向量共线定理就是什么？5、在物理中,力就是一个向量,力得合成就就是向量得加法运算、力也可以分解,任何一个大小不为零得力,都可以分解成两个不同方向得分力之与、将这种力得分解拓展到向量中来,就会形成一个新得数学理论、平面向量基本定理与正交分解及坐标表示探究(一):平面向量基本定理思考2:如图,设OA,OB,OC为三条共点射线,P为OC上一点,能否在OA、OB上分别找一点M、N,使四边形OMPN为平行四边形？思考7:根据上述分析,平面内任一向量a都可以由这个平面内两个不共线得向量e1,e2表示出来,从而可形成一个定理、您能完整地描述这个定理得内容吗？思考8:上述定理称为平面向量基本定理,不共线向量e1,e2叫做表示这一平面内所有向量得一组基底、那么同一平面内可以作基底得向量有多少组？不同基底对应向量a得表示式就是否相同？探究(二):平面向量得正交分解及坐标表示思考2:如果向量a与b得夹角就是90°,则称向量a与b垂直,记作a⊥b、互相垂直得两个向量能否作为平面内所有向量得一组基底？思考3:把一个向量分解为两个互相垂直得向量,叫做把向量正交分解、如图,向量i、j就是两个互相垂直得单位向量,向量a与i得夹角就是30°,且|a|=4,以向量i、j为基底,向量a如何表示？思考4:在平面直角坐标系中,分别取与x轴、y轴方向相同得两个单位向量i、j作为基底,对于平面内得一个向量a,由平面向量基本定理知,有且只有一对实数x、y,使得a＝xi＋yj、我们把有序数对(x,y)叫做向量a得坐标,记作a＝(x,y)、其中x叫做a在x轴上得坐标,y叫做a在y轴上得坐标,上式叫做向量得坐标表示、那么x、y得几何意义如何？思考5：相等向量的坐标必然相等，作向量a，则(x，y)，此时点A是坐标是什么？理论迁移例2如图,写出向量a,b,c,d得坐标、小结作业3、向量得坐标表示就是一种向量与坐标得对应关系,它使得向量具有代数意义、将向量得起点平移到坐标原点,则平移后向量得终点坐标就就是向量得坐标、2、3、3平面向量得坐标运算问题提出3、用坐标表示向量,使得向量具有代数特征,并且可以将向量得几何运算转化为坐标运算,为向量得运算拓展一条新得途径、我们需要研究得问题就是,向量得与、差、数乘运算,如何转化为坐标运算,对于共线向量如何通过坐标来反映等、平面向量得坐标运算及向量共线得坐标表示探究(一):平面向量得坐标运算思考2:根据向量得坐标表示,向量a＋b,a－b,λa得坐标分别如何？思考3:如何用数学语言描述上述向量得坐标运算？o思考6：若向量a=(x，y)，则|a|如何计算？若点A(x1,y1)，B(x2，y2)，则如何计算？探究(二):平面向量共线得坐标表示a理论迁移例2如图，已知ABCD的三个顶点的坐标分别是A（-2，1）、B（-1,3）、C(3,4)，试求顶点D的坐标.