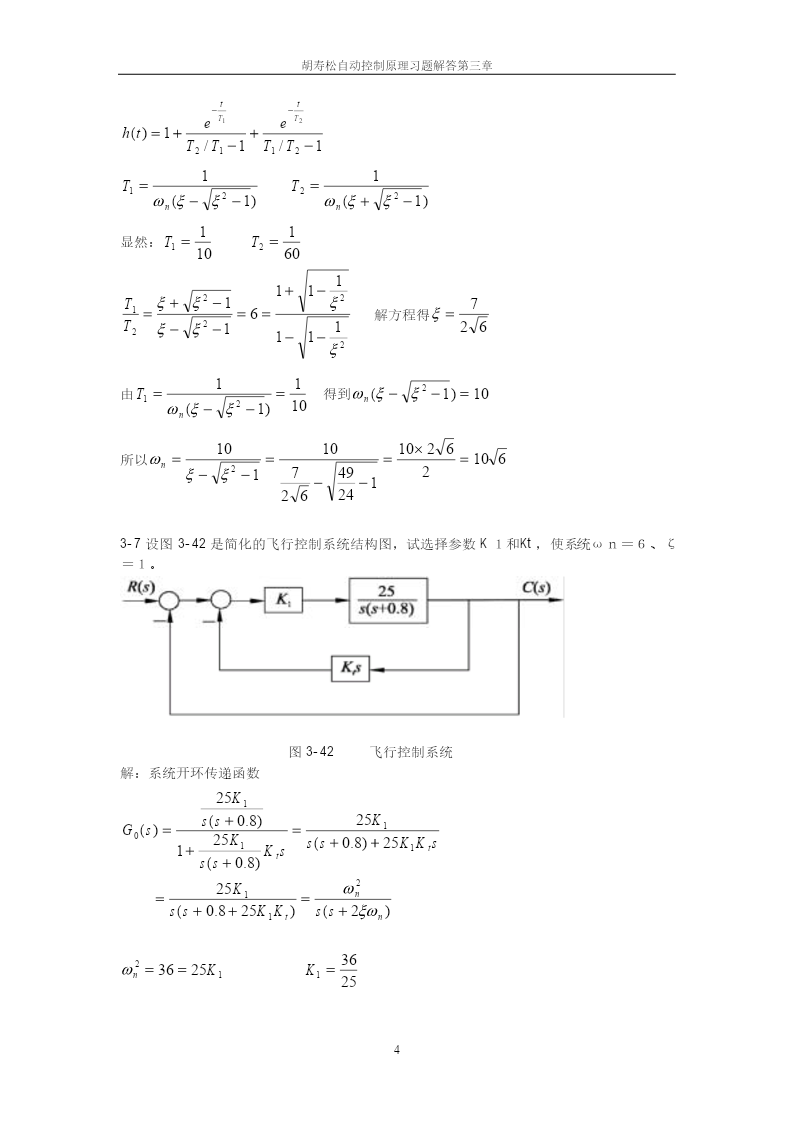
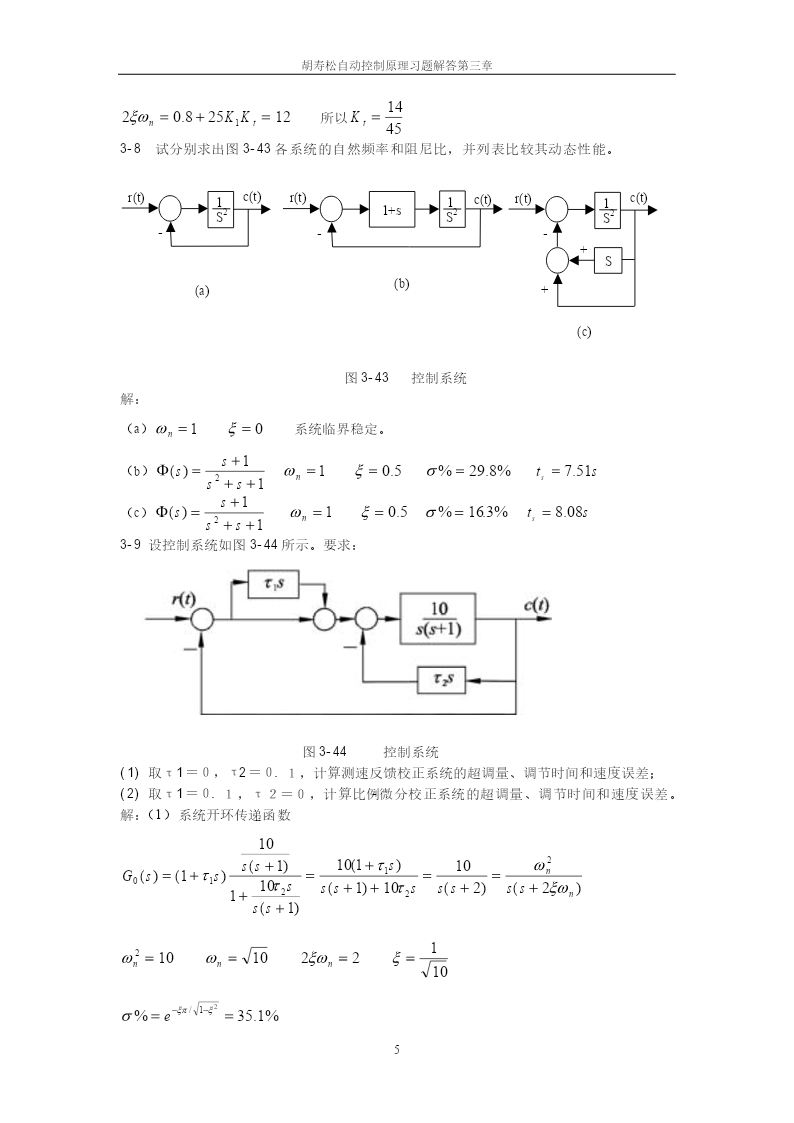
胡寿松自动控制原理习题解答第三章设随动系统的微分方程为：3-1T&x&0+x&0=K2uu=K1[r(t)−xf]Tfx&f+xf=x0其中T,Tf,K2为正常数。如果在外作用r(t)=1+t的情况下，使x0对r(t)的稳态误差不大于正常数ε0,试问k1应满足什么条件？见习题3-20解答3-2设系统的微分方程式如下：（1）0.2c&(t)=2r(t)（2）0.04c&&(t)+0.24c&(t)+c(t)=r(t)试求系统的单位脉冲响应k(t)和单位阶跃响应h(t)。已知全部初始条件为零。解：（1）因为0.2sC(s)=2R(s)单位脉冲响应：C(s)=10/sk(t)=10t≥0单位阶跃响应h(t)C(s)=10/s2h(t)=10tt≥0R(s)（2）(0.04s2+0.24s+1)C(s)=R(s)C(s)=0.04s2+0.24s+1125单位脉冲响应：C(s)=k(t)=e−3tsin4t0.04s2+0.24s+13251s+6单位阶跃响应h(t)C(s)==−s[(s+3)2+16]s(s+3)2+163h(t)=1−e−3tcos4t−e−3tsin4t43-3已知系统脉冲响应如下，试求系统闭环传递函数Φ（ｓ）。（1）k(t)=0.0125e−1.25t（2）k(t)=5t+10sin(4t+450)（3）k(t)=0.1(1−e−t/3)解：0.0125（1）Φ(s)=s+1.251胡寿松自动控制原理习题解答第三章（2）k(t)=5t+10sin4tcos450+10cos4tsin45054s5s+4Φ(s)=+52+52=+52s2s2+16s2+16s2s2+160.10.1（3）Φ(s)=−ss+1/33-4已知二阶系统的单位阶跃响应为h(t)=10−12.5e−1.2tsin(1.6t+53.1o)试求系统的超调量σ％、峰值时间ｔp和调节时间ｔs。1−ξωnt2解：h(t)=1−esin(1−ξωnt+β)1−ξ22π3.5β=arccosξσ%=e−πξ/1−ξt=t=p2sξω1−ξωnnξ=cosβ=cos53.10=0.6222σ%=e−πξ/1−ξ=e−π0.6/1−0.6=e−π0.6/1−0.6=9.5%ππt===1.96(s)p21.61−ξωn3.53.5ts===2.92(s)ξωn1.23-5设单位反馈系统的开环传递函数为0.4s+1G(s)=s(s+0.6)试求系统在单位阶跃输入下的动态性能。解：闭环传递函数0.4s+1G(s)s(s+0.6)0.4s+1G(s)===B0.4s+121+G(s)1+s+s+1s(s+0.6)10.4s+10.41C(s)=G(s)R(s)==+Bss2+s+1s2+s+1s(s2+s+1)0.41s+11s+0.6=+−=−s2+s+1ss2+s+1ss2+s+12胡寿松自动控制原理习题解答第三章32×0.63c(t)=1−e−0.5tcost−e−0.5tsint2233=1−1.22e−0.5tsin(t+55.30)21−ξωnt2h(t)=1−esin(1−ξωnt+β)1−ξ22π3.5β=arccosξσ%=e−πξ/1−ξt=t=p2sξω1−ξωnnξ=cosβ=cos55.30=0.5692σ%=e−πξ/1−ξ=11.37%ππ×2t===3.63sp21−ξωn33.53.5ts===7sξωn0.53-6已知控制系统的单位阶跃响应为h(t)=1+0.2e−60t−1.2e−10t试确定系统的阻尼比ζ和自然频率ωｎ。解：求拉氏变换得10.21.2(s+60)(s+10)0.2s(s+10)1.2s(s+60)H(s)=+−=+−ss+60s+10s(s+60)(s+10)s(s+60)(s+10)s(s+60)(s+10)2600600ωn==2=22s(s+60)(s+10)s(s+70s+600)s(s+2ξωns+ωn)ω2显然闭环传递函数为n22(s+2ξωns+ωn)7其中ω2=600ω=1062ξω=70ξ=nnn26根据（3-17）e−t/T1e−t/T12h(t)=1++T2/T1−1T1/T2−1解：根据公式（3-17）3胡寿松自动控制原理习题解答第三章tt−−eT1eT2h(t)=1++T2/T1−1T1/T