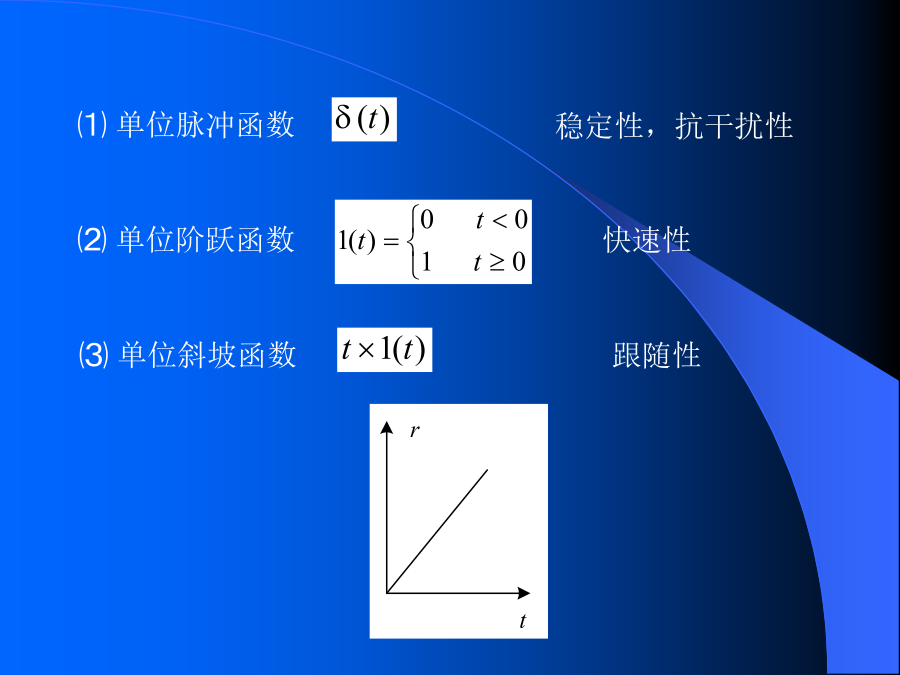
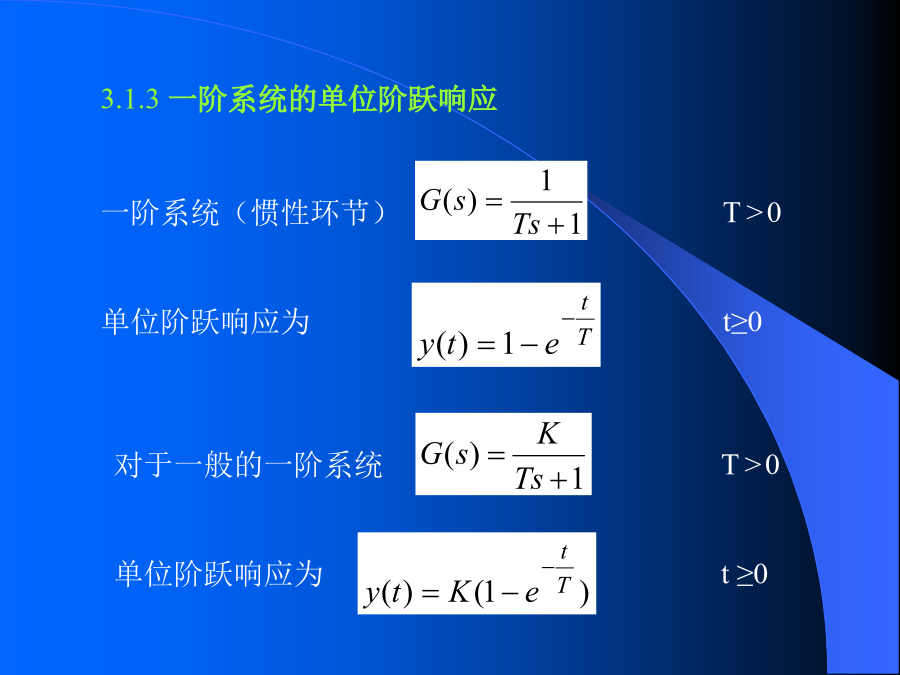
第三章控制系统的时域分析⑴单位脉冲函数⑷单位加速度函数跟随性3.1.2动态性能指标设零初始状态，y(0)=0ym：单位阶跃响应的最大偏离量。重要的指标：注意：输入信号为非单位阶跃信号时，依齐次性，响应只是沿纵轴拉伸或压缩，基本形状不变。所以ts、tr、tp、σ并不发生变化。3.1.3一阶系统的单位阶跃响应3.1.4二阶系统的单位阶跃响应单位反馈时结构图单位阶跃响应为Re2．临界阻尼ζ=1Re3．欠阻尼0＜ζ＜1①超调量：4．无阻尼ζ=0t解：化标准型为3.1.5高阶系统的单位阶跃响应单位阶跃响应为高阶系统的分析方法：例，两个系统为和分别求它们在零初始状态下的单位阶跃响应。解：输出的拉氏变换分别为对比两式可以看出，极点决定衰减项的时间常数，零点决定衰减项的系数。G2(s)：例2系统的传递函数为，求零初始状态下的单位阶跃响应。解：输出的拉氏变换为令上式中则响应为增加一个极点，则增加一个暂态分量。例，系统传递函数为试分析阶跃响应的动态性能。其中极点10是非主导极点，可以消去；极点3和零点3.2相距很近，也可以消去。传递函数的化简应在保持静态增益不变的前提下进行，即有其参数和阶跃响应的性能指标为由本例可以体会到，把高阶系统近似为简单的一阶或二阶系统将大大有利于对系统的分析。这种方法能看出响应的性质（单调上升还是衰减振荡），又能很快计算出性能指标，还能对改进系统提供依据。注意：离虚轴很近的一对零、极点通常是不能消去的。这是因为这一对零、极点各自对暂态分量的贡献都很大；由于数学模型不可避免的误差，它们实际上也许不太符合对消的条件，这时，对消带来的误差将给结论带来本质性的影响。至于不稳定的极点，就更不允许对消了。3.1.7附加零极点的影响3.2控制系统的稳态精度，性能指标3.2.2给定稳态误差由拉氏变换的终值定理得：表示为：1.单位阶跃函数输入时，稳态误差常称为位置误差。输入r(t)=1(t)，R(s)=1/s当=0（称为0型系统），则位置误差系数和位置误差分别为2．单位斜坡函数输入时，稳态误差称为速度误差，输入r(t)=t1(t)，R(s)=1/s2，故当=0时，速度误差系数和速度误差分别为3.单位加速度函数输入时，稳态误差称为加速度误差当时，加速度误差系数和加速度误差分别为例，结构图1型系统，开环增益K=4/3。由表4-1得位置误差=0速度误差=1/K=3/4加速度误差=3.2.3有扰动输入时稳态误差①给定输入误差（n=0时）K=1v=11型系统，可以查表此时由于Gk(s)的意义不适合扰动输入，（Gk(s)是e-b之间），所以不能直接查表。③总的误差：3.3根轨迹分析由于Gk(s)比Gb(s)较简单，所以希望能通过Gk(s)来研究Gb(s)特征根的分布情况。闭环特征方程为当K*=0时，Gk(s)的极点也是Gb(s)的极点。例，单位反馈系统的开环传递函数为闭环系统特征方程为：根轨迹图中的“×”表示开环极点；“0”表示开环零点。根轨迹上的箭头表示K*增大的方向。（1）当K*<0.385时，闭环系统有两个实数主导极点，动态性能近似为过阻尼无零点二阶系统，无超调。(3)当K*=1.06时,根轨迹上相应的点与实轴的夹角约为60，实部约为0.4，阻尼系数约为cos60=0.5（4）当K*>6时，闭环系统不稳定。3.3.3根轨迹方程幅值条件：要点：例，；对于根，求K*。3.3.4绘制根轨迹法则1.分支数和对称性：n阶系统有n支根轨迹，对称于实轴。例34.分离点和会合点：分离点和会合点是下面方程的部分或全部的解：两支根轨迹的分离角和会合角为90度，它是分离点和会合点切线与实轴的夹角。例，；画出根轨迹得：例得：x=-2.12，0.12；0.12不在实轴的根轨迹区域内。取x=-2.12做会合点。5.闭环极点之和：如果n-m≥2，则闭环极点之和等于开环极点之和。由于开环极点之和为定值，则闭环极点之和也为定值。6.渐近线：当根轨迹趋于无穷远时，有渐近线，渐近线的条数为n-m条。例画根轨迹。得x=-0.42，-1.6；-1.6不在实轴的根轨迹区域内。取x=-0.42作为分离点。交角=例7，上例令其根为纯虚数s=jω，代入上式：3.3.5根轨迹分析Re2.由开环传递函数中的参数来分析对闭环系统动态性能的影响，属于定性分析此形式看不出τ对系统的影响。实际是有影响的，但此形式不明显。下面作一个变换，变成易于看出τ影响的形式。等式两边同除得画根轨迹分析τ变化对稳态性能e(∞)的影响，将原结构图变形为：3.改变开环传递函数来改变闭环动态性能，定性分析3.4前馈补偿3.4.1按扰动的前馈补偿假设G0和G1之间是可加入信号的距N加入点最近的加入点。选择补偿信号加