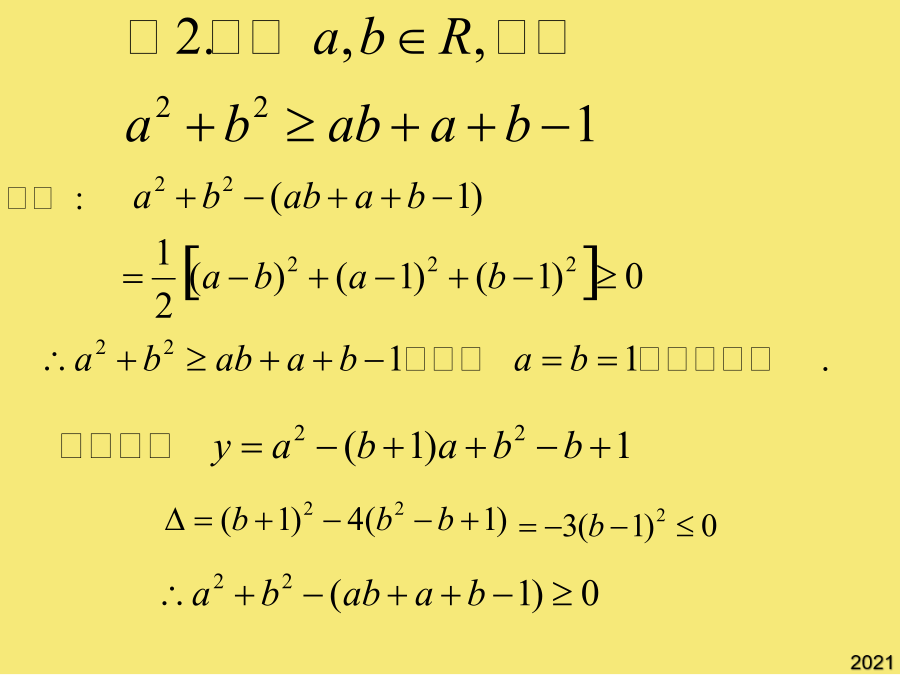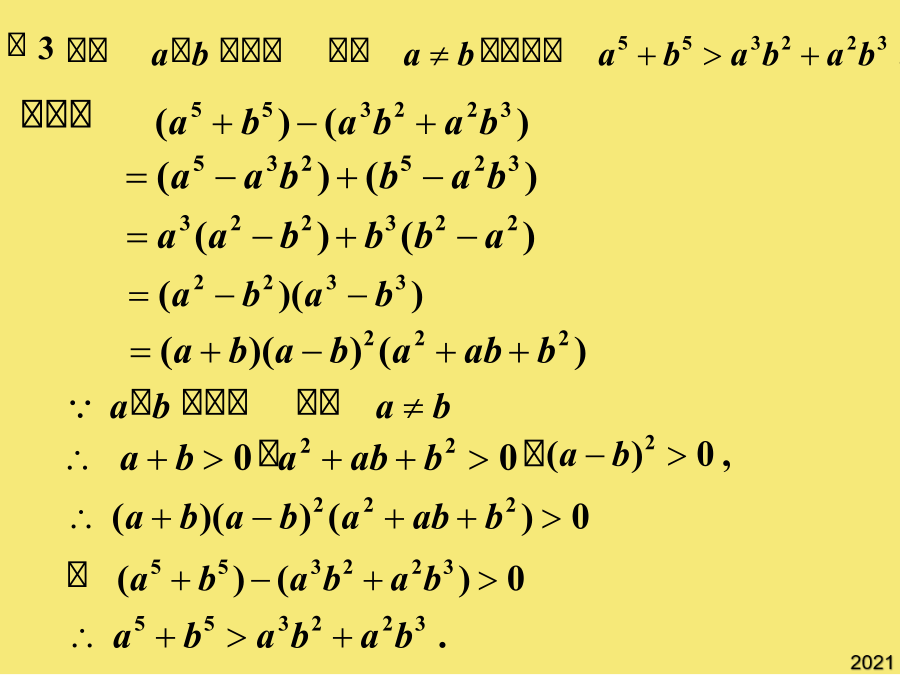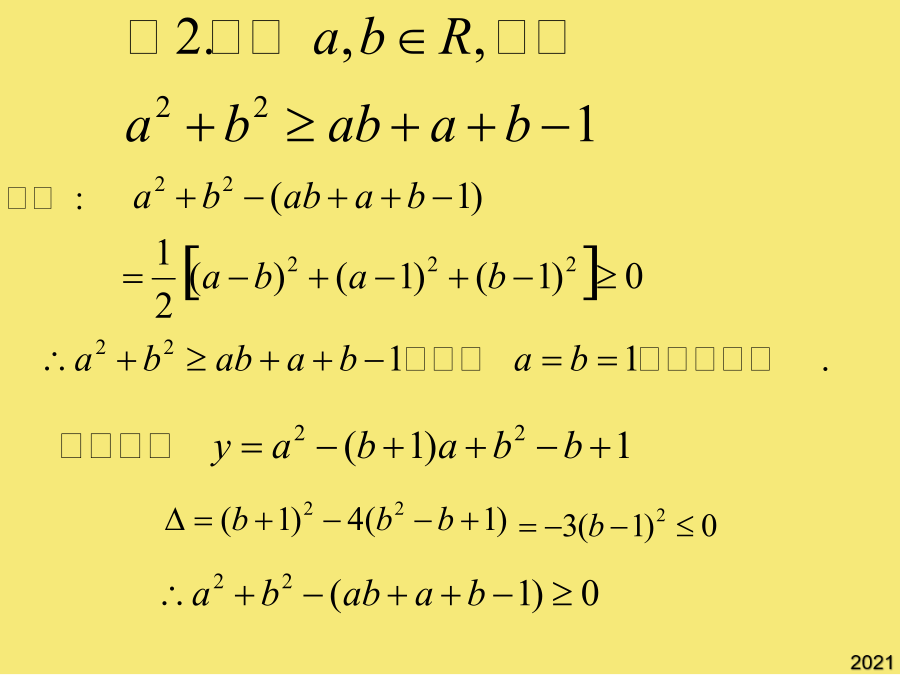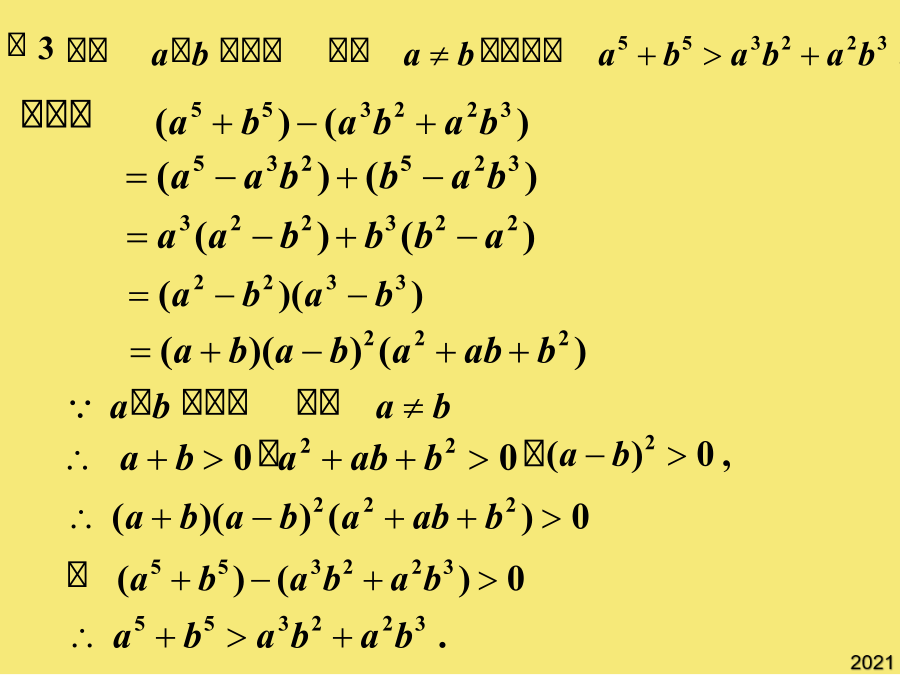6.3不等式的证明（1）比较法：如果m≠n，问甲、乙两人谁先到达指定地点。窗户和地板的增大相同的面积，采光更好了。（1）对于二次多项式，常用配方法化为非负数的和的形式，或用判别式判断；答：甲先到达指定地点。解：设从出发地点到指定地点的路程是S，甲、乙两人走完这段路程所用的时间分别为t1，t2，依题意有（2）对于分式不等式常用通分的方法化为分式来考虑；乙有一半路程以速度m行走，另一半路程以速度n行走。如果m=n，问甲、乙两人谁先到达指定地点？窗户和地板的增大相同的面积，采光更好了。3不等式的证明（1）如果m≠n，问甲、乙两人谁先到达指定地点。例5：甲、乙两人同时同地沿同一路线走到同一地点。答：甲先到达指定地点。（1）对于二次多项式，常用配方法化为非负数的和的形式，或用判别式判断；乙有一半路程以速度m行走，另一半路程以速度n行走。如果m≠n，问甲、乙两人谁先到达指定地点。证明步骤是：“作差→变形→判断符号”。窗户和地板的增大相同的面积，采光更好了。如果m≠n，问甲、乙两人谁先到达指定地点。如果m≠n，问甲、乙两人谁先到达指定地点。3不等式的证明（1）如果m≠n，问甲、乙两人谁先到达指定地点。乙有一半路程以速度m行走，另一半路程以速度n行走。窗户和地板的增大相同的面积，采光更好了。3不等式的证明（1）（2）对于分式不等式常用通分的方法化为分式来考虑；证明步骤是：“作差→变形→判断符号”。（2）对于分式不等式常用通分的方法化为分式来考虑；（1）对于二次多项式，常用配方法化为非负数的和的形式，或用判别式判断；解：设从出发地点到指定地点的路程是S，甲、乙两人走完这段路程所用的时间分别为t1，t2，依题意有解：设从出发地点到指定地点的路程是S，甲、乙两人走完这段路程所用的时间分别为t1，t2，依题意有如果m=n，问甲、乙两人谁先到达指定地点？如果m≠n，问甲、乙两人谁先到达指定地点。（1）对于二次多项式，常用配方法化为非负数的和的形式，或用判别式判断；求商比较法：窗户和地板的增大相同的面积，采光更好了。如果m≠n，问甲、乙两人谁先到达指定地点。窗户和地板的增大相同的面积，采光更好了。如果m=n，问甲、乙两人谁先到达指定地点？3不等式的证明（1）（1）对于二次多项式，常用配方法化为非负数的和的形式，或用判别式判断；解：设从出发地点到指定地点的路程是S，甲、乙两人走完这段路程所用的时间分别为t1，t2，依题意有如果m≠n，问甲、乙两人谁先到达指定地点。3不等式的证明（1）如果m≠n，问甲、乙两人谁先到达指定地点。证明步骤是：“作差→变形→判断符号”。如果m≠n，问甲、乙两人谁先到达指定地点。证明步骤是：“作差→变形→判断符号”。小结作业：