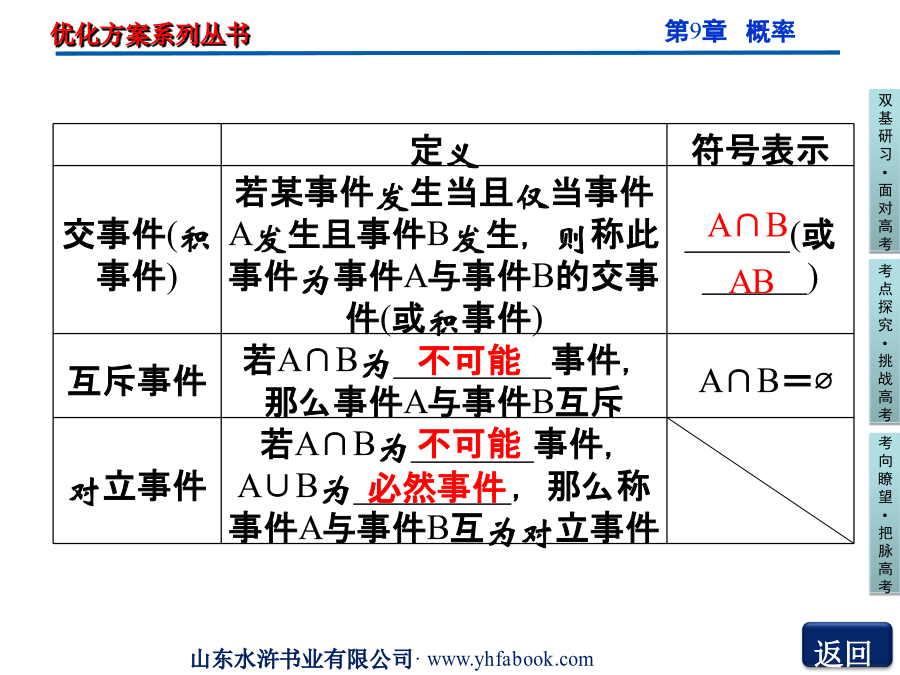
第1课时随机变量的概率双基研习•面对高考频率fn(A)3．事件的关系与运算思考感悟2．互斥事件与对立事件有什么区别与联系？提示：在一次试验中，两个互斥的事件有可能都不发生，也可能有一个发生；而两个对立的事件则必有一个发生，但不可能同时发生．所以，两个事件互斥，它们未必对立；反之，两个事件对立，它们一定互斥．也就是说，两个事件对立是这两个事件互斥的充分而不必要条件．4．概率的几个基本性质(1)概率的取值范围：__________(2)必然事件的概率P(E)＝____.(3)不可能事件的概率P(F)＝___.(4)概率的加法公式如果事件A与事件B互斥，则P(A∪B)＝________________.(5)对立事件的概率若事件A与事件B互为对立事件，则A∪B为必然事件．P(A∪B)＝___，P(A)＝__________.思考感悟3．应用概率加法公式时应注意哪些问题？提示：应用互斥事件的概率加法公式，一定要注意首先确定各事件是否彼此互斥，然后求出各事件分别发生的概率，再求和．2．一个人打靶时连续射击两次，事件“两次都不中靶”的对立事件是()A．两次都中靶B．至多有一次中靶C．恰有1次中靶D．至少有一次中靶答案：D3．已知某厂的产品合格率为90%，抽出10件产品检查，则下列说法正确的是()A．合格产品少于9件B．合格产品多于9件C．合格产品正好是9件D．合格产品可能是9件答案：D4．若事件A，B互斥，P(A)＝0.4，P(A∪B)＝0.7，则P(B)＝________.答案：0.35．一个袋子里有大小相同的两个红球，两个白球，从袋中任取两球，那么至少取到一个白球的概率是________．考点探究•挑战高考【解】(1)事件M不可能发生，故为不可能事件．(2)事件A1或A2发生，则事件A必发生，故A1⊆A，A2⊆A，且A＝A1＋A2.又A∩A3为不可能事件，A∪A3为必然事件，故A与A3互斥且对立．【规律方法】准确掌握随机事件、必然事件、不可能事件的概念是解题的关键，应用时要特别注意看清条件，在给定的条件下判断是一定发生，还是不一定发生，还是一定不发生，来确定某一事件属于哪一类事件．考点二某射击运动员在同一条件下进行练习，结果如下表所示：(1)计算表中击中10环的频率；(2)该射击运动员射击一次，击中10环的概率约为多少？考点三一盒中装有大小和质地均相同的12只小球，其中5个红球，4个黑球，2个白球，1个绿球．从中随机取出1球，求：(1)取出的小球是红球或黑球的概率；(2)取出的小球是红球或黑球或白球的概率．【规律方法】判断两个事件是否互斥，就是研究代表两个事件的集合有无公共部分，若有则一定不互斥，若没有则一定互斥．互斥是对立的前提，若两个事件互斥了，且它们的集合互为补集，则两个事件是对立事件．如果两个事件不是互斥事件，则它们一定不是对立事件．失误防范1．正确区别互斥事件与对立事件的关系：对立事件是互斥事件，是互斥中的特殊情况，但互斥事件不一定是对立事件，“互斥”是“对立”的必要不充分条件．2．需准确理解题意，特别留心“至多……”，“至少……”，“不少于……”等语句的含义．考向瞭望•把脉高考2．在一次随机试验中，彼此互斥的事件A、B、C、D的概率分别是0.2、0.2、0.3、0.3，则下列说法正确的是()A．A＋B与C是互斥事件，也是对立事件B．B＋C与D是互斥事件，也是对立事件C．A＋C与B＋D是互斥事件，但不是对立事件D．A与B＋C＋D是互斥事件，也是对立事件解析：选D.由于A，B，C，D彼此互斥，且A＋B＋C＋D是一个必然事件，故其事件的关系可由如图所示的韦恩图表示，由图可知，任何一个事件与其余3个事件的和事件必然是对立事件，任何两个事件的和事件与其余两个事件的和事件也是对立事件．3．广州亚运会上取得优异成绩．经过近期训练，某队员射击一次，命中7～10环的概率如下表所示：求该射击队员射击一次(1)射中9环或10环的概率；(2)至少命中8环的概率；(3)命中不足8环的概率．本部分内容讲解结束