如果您无法下载资料,请参考说明:
1、部分资料下载需要金币,请确保您的账户上有足够的金币
2、已购买过的文档,再次下载不重复扣费
3、资料包下载后请先用软件解压,在使用对应软件打开
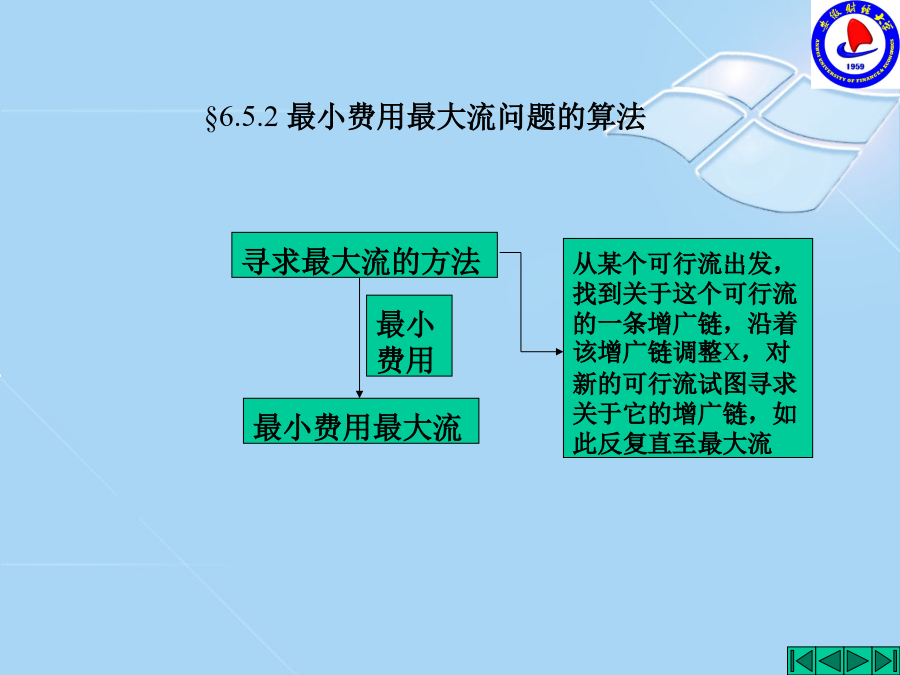
+5在D中找对应的增广链0000000.0000000.for(nodes(i)|i#ne#1#and#i#ne#size(nodes):C(2,1)2.这样,D就成为一个带费用的网络,记为D=(V,A,W,C),0000000.设网络D=(V,A,W),[x,fval,exitflag,output,lambda]=linprog(g,[],[],aeq,beq,lb,ub);U(2,3)3.0000000.C(1,T)1.故最终可得一条过G中所有即得G中的一条连接u,v的欧拉链。而把D中的每一条弧最大流为:3+8=7+4=11sets:nodes/s,1,2,3,t/:d;arcs(nodes,nodes)/s,1s,22,12,31,t1,33,t/:c,u,f;endsetsdata:d=11000-11;c=4123162;u=108510724;enddatamin=sum(arcs:c*f);for(nodes(i)|i#ne#1#and#i#ne#size(nodes):sum(arcs(i,j):f(i,j))-sum(arcs(j,i):f(j,i))=d(i));sum(arcs(i,j)|i#eq#1:f(i,j))=d(1);for(arcs:bnd(0,f,u));Globaloptimalsolutionfoundatiteration:2Objectivevalue:55.00000VariableValueReducedCostD(S)11.000000.000000D(1)0.0000000.000000D(2)0.0000000.000000D(3)0.0000000.000000D(T)-11.000000.000000C(S,1)4.0000000.000000C(S,2)1.0000000.000000C(2,1)2.0000000.000000C(2,3)3.0000000.000000C(1,T)1.0000000.000000C(1,3)6.0000000.000000C(3,T)2.0000000.000000U(S,1)10.000000.000000U(S,2)8.0000000.000000U(2,1)5.0000000.000000U(2,3)10.000000.000000U(1,T)7.0000000.000000U(1,3)2.0000000.000000U(3,T)4.0000000.000000F(S,1)3.0000000.000000F(S,2)8.000000-1.000000F(2,1)4.0000000.000000F(2,3)4.0000000.000000F(1,T)7.000000-2.000000F(1,3)0.0000005.000000F(3,T)4.0000000.000000000000D(4)0.可以看出,最小费用最大流问题其实就是在最故可用Dijkstra算法求得最短路为桥回到原出发点,且每座桥只走一次。nodes/1,2,3,4,5/:d;C(2,4)5.0000000.当可行流增加单位流值时费D(1)0.C(1,T)1.0000003.sum(arcs(i,j)|i#eq#1:f(i,j))=d(1);0,0,1,0,1,-1,0];的所有可行流中的最小费用流,000000-7.要从邮局出发走遍负责的所有街道,谢谢