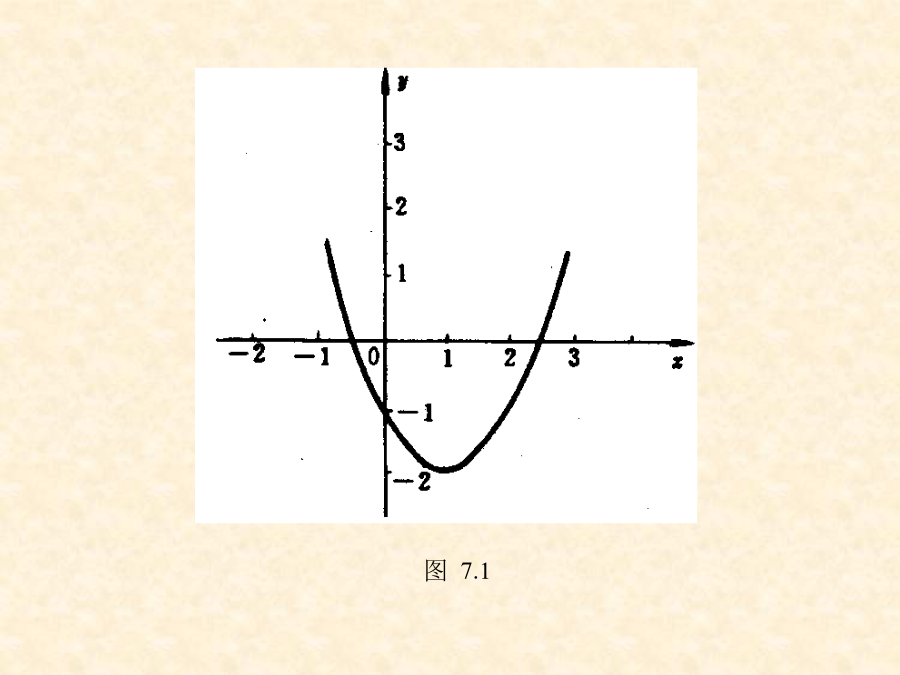
§1方程求根与二分法则可用搜索法求有根区间.方程根的数值计算大致可分三个步骤进行:(1)判定根的存在性。(2)确定根的分布范围,即将每一个根用区间隔离开来。(3)根的精确化,即根据根的初始近似值按某种方法逐步精确化,直至满足预先要求的精度为止。设f(x)为定义在某区间上的连续函数,方程(1.1)存在实根。虽然方程(1.1)的根的分布范围一般比较复杂,但我们不难将函数f(x)的定义域分成若干个只含一个实根的区间。例如考虑方程x2-2x-1=0由图7.1所示,该方程的一个负实根在-1和0之间,另一个正实根在2和3之间。图7.1这样,我们总可以假设方程(1.1)在(a,b)内有且仅有一个单实根x*。由连续函数的介值定理知f(a)·f(b)＜0若数值b-a较小,那么我们可在(a,b)上任取一点x0作为方程的初始近似根。例如,方程f(x)=x3-x-1=0由于f(1)＜0,f(1.5)＞0,又f(x)在区间(1,1.5)上单调连续,故可知在(1,1.5)内有且仅有一个实根。于是可取某个端点或区间内某一个点的值作为根的初始近似值。设函数f(x)在区间［a,b］上单调连续,且f(a)·f(b)＜0则方程(1.1)在区间(a,b)内有且仅有一个实根x。二、二分法1.计算步骤①输入有根区间的端点a,b及预先给定的精度ε;②(a+b)/2x;③若f(a)f(x)＜0,则x=b,转向④;否则x=a,转向④。④若b-a＜ε,则输出方程满足精度的根x,结束;否则转向②。图7.22.计算框图(见下页）例1求方程f(x)=x3-x-1=0在区间(1,1.5)内的根。要求用四位小数计算,精确到小数点后两位。解这里a=1,b=1.5，取区间(1,1.5)的中点取x6=1.3242，误差限|x6-x*|<0.5/(2^7)<0.005,故x6即为所求近似根，实际上根x*=1.324717…二分法优点：计算简单，收敛性有保证；二分法缺点：收敛不够快，特别是精度要求高时，工作量大，而且不能够求复根及双重根。§2迭代法如果点列﹛Pk﹜趋向于点P*，则相应的迭代值xk收敛到所求根x*.k虽然迭代法的基本思想很简单,但效果并不总是令人满意的。对于上例,若按方程写成另一种等价形式x=x3-1建立迭代公式xk+1=x3k-1,k=0,1,2,…仍取初始值x0=1.5,则迭代结果为x1=2.375x2=12.3976这种不收敛的迭代过程称作是发散的。如下图：二、不动点的存在性与迭代法的收敛性三、局部收敛性与收敛阶证明由连续函数的性质，存在x*的某个邻域R：|x-x*|≤δ，使对于任意x∈R成立|ψ＇(x)|≤L<1.此外，对于任意x∈R，总有ψ(x)∈R，这是因为|ψ(x)-x*|=|ψ(x)-ψ(x*)|≤L|x-x*|≤|x-x*|≤δ.于是依据定理2可以断定迭代过程xk+1=ψ(xk)对于任意初值x0∈R均收敛.证毕.k§3迭代收敛的加速方法二、斯蒂芬森迭代法kk§4牛顿法牛顿法是非线性方程线性化的方法。其计算步骤为:①给出初始近似根x0及精度ε。②计算③若｜x1-x0｜＜ε,则转向④;否则,转向②。④输出满足精度的根x1,结束。牛顿法的计算框图见图7.4。图7.4牛顿法有明显的几何解释，方程f(x)=0的根x*可解释为曲线y=f(x)与x轴的交点的横坐标.设xk是跟x*的某个近似值,过曲线y=f(x)上横坐标为xk的点Pk引切线,并将该切线与x轴的交点的横坐标xk+1作为x*的新的近似值.注意到切线方程为y=f(xk)+f＇(xk)(x-xk).这样求得的值xk+1必满足（4.1）式，从而就是牛顿公式（4.2）的计算结果.由于这种几何背景,牛顿法亦称为切线法.二、牛顿法应用举例三、简化牛顿法与牛顿下山法k四、重根情形k§5弦截法k例11用抛物线法求解方程f(x)=xex-1=0.§6求根问题的敏感性与多项式的零点（a）良态谢谢