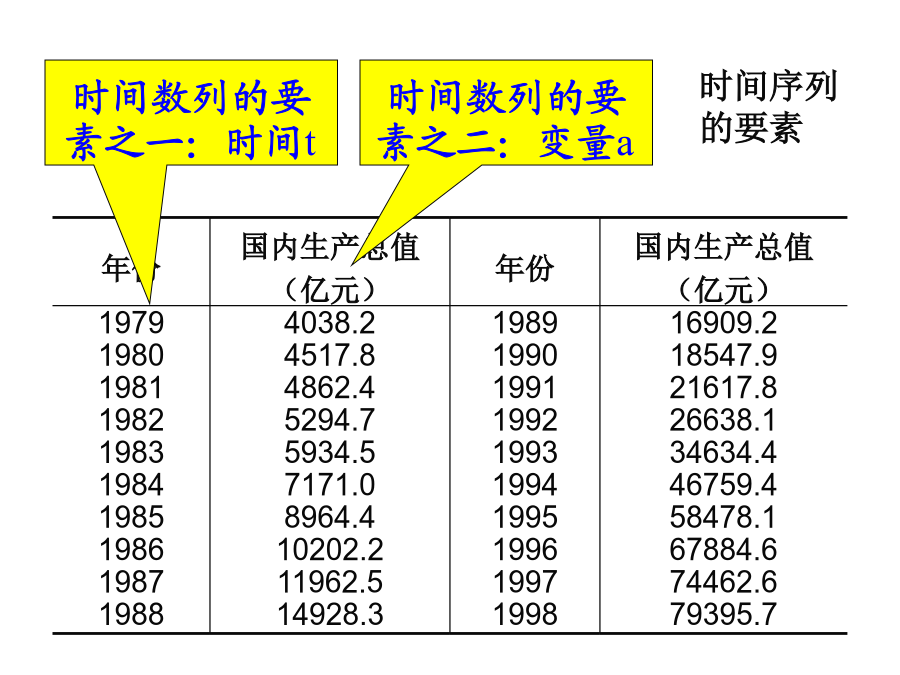
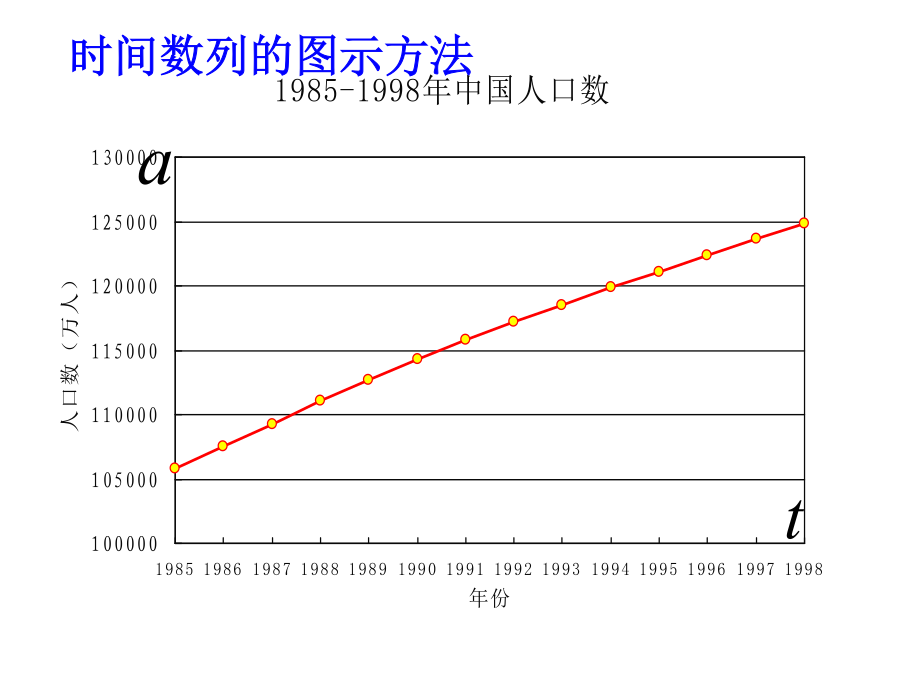
§3.3时间序列分析教学要求一、时间序列分析的基本原理重要概念年份时间数列的图示方法编制时间数列的意义（二）时间序列的组合成份长期趋势（T）是指时间序列随时间的变化而逐渐增加或减少的长期变化的趋势。季节变动（S）是指时间序列在一年中或固定时间内，呈现出的固定规则的变动。循环变动（C）是指沿着趋势线如钟摆般地循环变动，又称景气循环变动(businesscyclemovement)。不规则变动（I）是指在时间序列中由于随机因素影响所引起的变动。（三）时间序列的组合模型二、趋势拟合方法(长期趋势分析)（一）平滑法滑动平均法其计算公式为式中:为t点的滑动平均值;l为单侧平滑时距。若l=1，则（3.3.4）式称为三点滑动平均，其计算公式为若l=2，则（3.3.4）式称为五点滑动平均，其计算公式为通过平均每一个连续数列值来修匀时间数列的方法。移动平均法的计算滑动平均法的计算原数列例题1使用移动/滑动平均法应注意的问题：可以平滑修匀数列；对于季节性数列，要采用4项或12项移动/滑动平均，方可平滑掉其季节波动；一般的移动平均方法使原数列首尾各去除了若干项，因此不能用于外推预测；当数列没有明显的长期趋势、季节变动和循环变动时，可以用此法进行预测。指数平滑法①一次指数平滑α为平滑系数。一般时间序列较平稳，α取值可小一些，一般取α∈（0.05,0.3）；若时间序列数据起伏波动比较大，则α应取较大的值，一般取α∈（0.7,0.95）。②高次指数平滑法一次指数平滑法不能跨期预测，对其进行改进，可以得到能够跨期预测的高次指数平滑法。令为一次指数平滑值，即对二次指数平滑再作一次指数平滑，可得三次指数平滑公式▲三次指数平滑法的预测公式为式中，例2：趋势线拟合法：用某种趋势线（直线或曲线）来对原数列的长期趋势进行拟合。其主要作用是进行外推预测。趋势线拟合法的基本程序判断趋势类型ttt用最小二乘法求a、b的公式：自相关性判断①时间序列的自相关，是指序列前后期数值之间的相关关系，对这种相关关系程度的测定便是自相关系数。②测度:设y1，y2，…，yt，…，yn，共有n个观察值。把前后相邻两期的观察值一一成对，便有（n－1）对数据，即(y1，y2)，(y2，y3)，…，(yt，yt+1)，…，(yn-1，yn)。其一阶自相关系数r1为k阶自相关系数为自回归模型的建立常见的线性自回归模型：①一阶线性自回归预测模型为②二阶线性自回归预测模型为③一般地，p阶线性自回归模型为在以上各式中，为待估计的参数值，它们可以通过最小二乘法估计获得。例3：某地区1988～1999年12年自然灾害造成的成灾面积（102hm2）的时间序列数据见表3.3.9。试计算该时间序列的自相关系数r1和r2，并用自回归模型预测2000年的成灾面积。说明：自由度f=11-2=9，在置信度水平α=0.001下查相关系数的临界值检验表得r0.001=0.8471，显然r1>r0.001。这表明一阶自相关系数r1具有高度的显著性。进一步检验发现，二阶自相关系数r2也是高度显著的。所以，对于该序列可以建立线性自回归模型。由于r1>r2，故可以建立一阶线性自回归预测模型。用最小二乘法估计模型参数，得到如下回归模型：运用该模型进行预测计算：三、季节变动预测季节变动（Seasonal）：一年之内因纯季节原因造成的数列的波动，以及与季节无关的类似的变动。测量季节变动的意义趋势剔除法的基本过程季节性预测法的具体步骤2）将原序列y除以其对应的趋势方程值（或平滑值），得到相对数数列,从而分离出季节变动（含不规则变动），即（3）计算相对数数列的平均水平.将月度（或季度）的季节指标加总，以由计算误差导致的值去除理论加总值，得到一个校正系数，并以该校正系数乘以季节性指标从而获得调整后季节性指标。（4）求预测模型，若求下一年度的预测值，延长趋势线即可；若求各月（季）的预测值，需以趋势值乘以各月份（季度）的季节性指标。求季节变动预测的数学模型（以直线为例）为式中：是t+k时的预测值;at、bt为方程系数;为季节性指标。例题：如表3.3.3所示，下面我们用上述步骤，预测该旅游景点2005年各季度的客流量。（2）求季节性指标：将表3.3.3中第4列数据分别除以第5列各对应元素，得相应的季节系数。然后再把各季度的季节系数平均得到季节性指标，见表.季节性指标之和理论上应等于4。现等于3.9515，需要进行校正。校正方法是：先求校正系数：θ=4/3.9515=1.0123。然后将表中的第4行，分别乘以θ，即得校正后的季节性指标（见表3.3.4第5行）。高次指数平滑法一次指数平滑法不能跨期预测，对其进行改进，可以得到能够跨