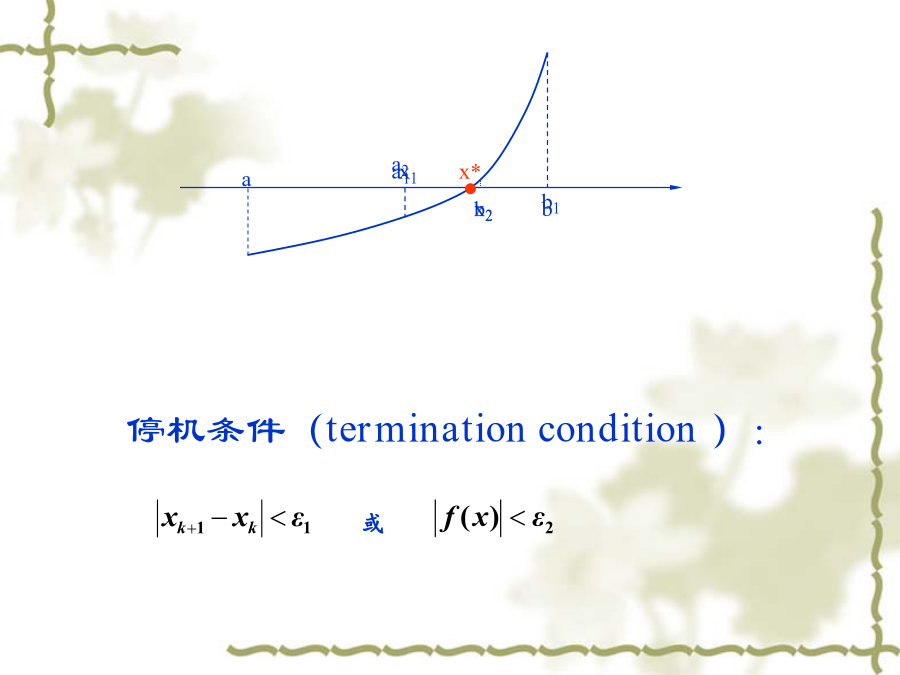
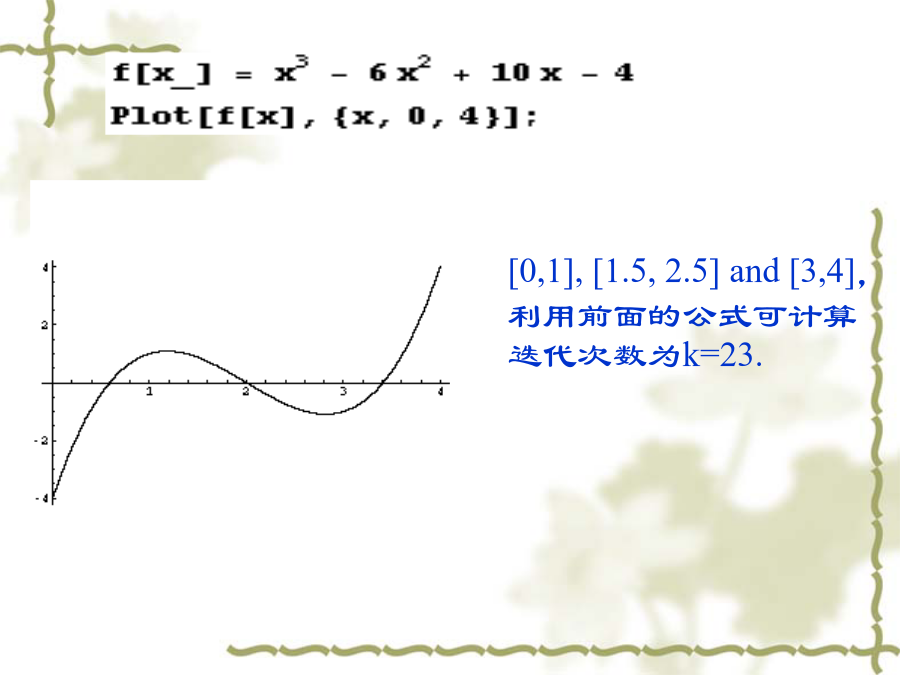
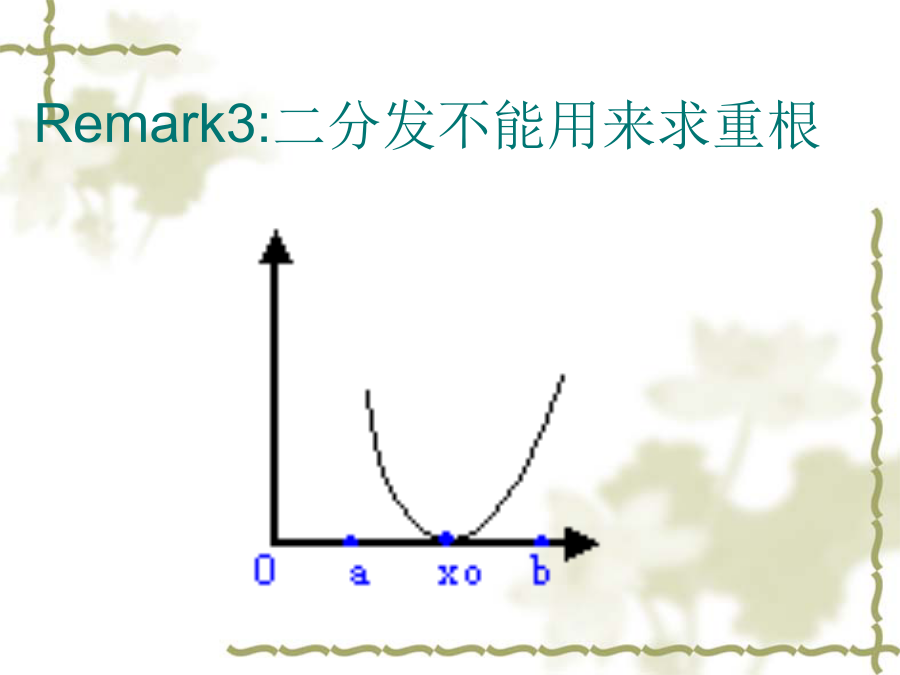
简介（Introduction）§3.1对分区间法(BisectionMethod)误差分析：例1用二分法求在(1,2)内的根，要求绝对误差不超过解：f(1)=-5<0有根区间中点f(2)=14>0-(1,2)+f(1.25)<0(1.25,1.5)f(1.375)>0(1.25,1.375)f(1.313)<0(1.313,1.375)f(1.344)<0(1.344,1.375)f(1.360)<0(1.360,1.375)f(1.368)>0(1.360,1.368)12Remark1：求奇数个根Remark2:要区别根与奇异点Remark3:二分发不能用来求重根f(x)=0(1)如果将原方程化为等价方程(2)如果将原方程化为等价方程收敛性分析考虑方程x=g(x),g(x)C[a,b],若(I)当x[a,b]时，g(x)[a,b]；(II)在［a,b］上成立不等式：|g(x1)-g(x2)|≤|x1-x2|。则（1）g在［a,b］上存在惟一不动点x*（2）任取x0[a,b]，由xk+1=g(xk)得到的序列{xk}（［a,b】）收敛于x*。（3）k次迭代所得到的近似不动点xk与精确不动点x*有有误差估计式：§3Fixed-PointIteration§3Fixed-PointIterationRemark：例题在这里我们考查在区间[3.5,4]的迭代法的收敛性局部收敛性定理举例例题将方程化为等价方程：x＝2＋lnx73.14614361183.14617745293.146188209103.146191628113.146192714123.146193060133.146193169143.146193204另一种迭代格式：程序演示定理3.2.3Prove:(3)由于g在x*处p阶连续可微且g(p)(x*)≠0，知必存在x*的某邻域Ｕ(x*)，当x∈U(x*)时，有g(p)(x)≠0.由于x*+(xk-x*)∈［x*-，x*+］U(x*)，故g(p)(x*+(xk-x*))≠0，k=0，1,2,….可见，当初值x0≠x*时，由(11)式可推出诸xk≠x*于是由(11)式有作业（homework)