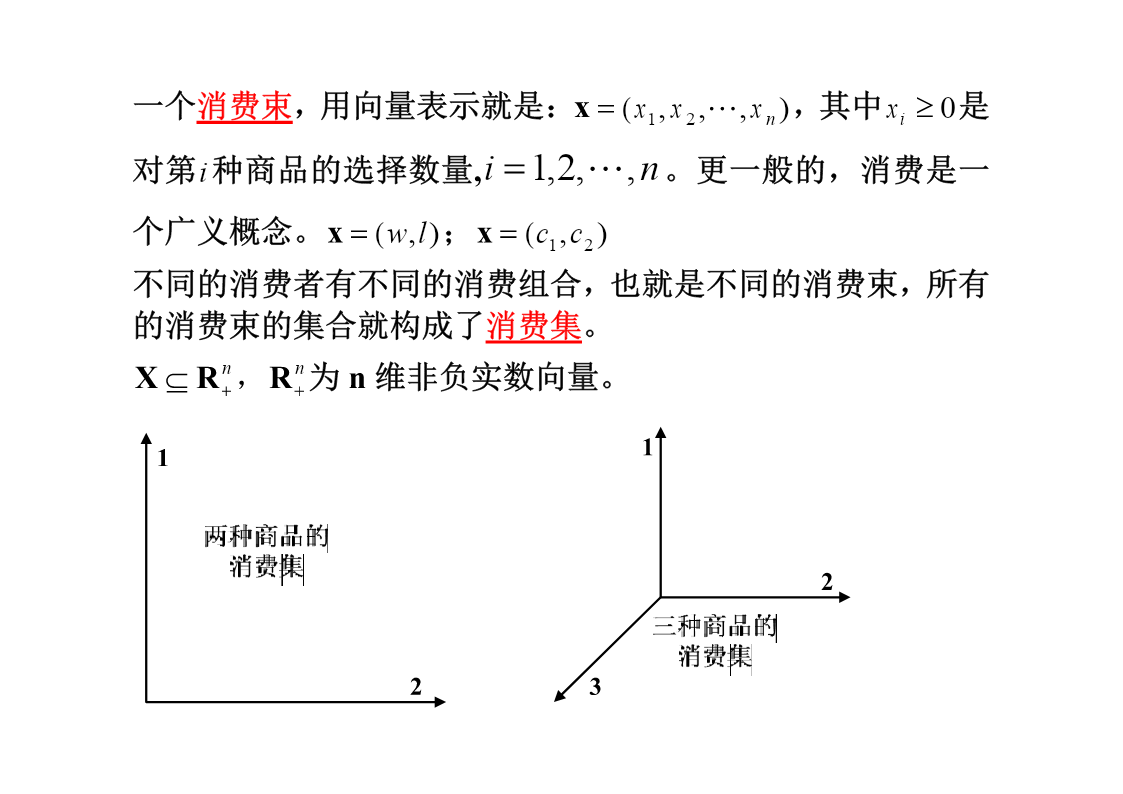
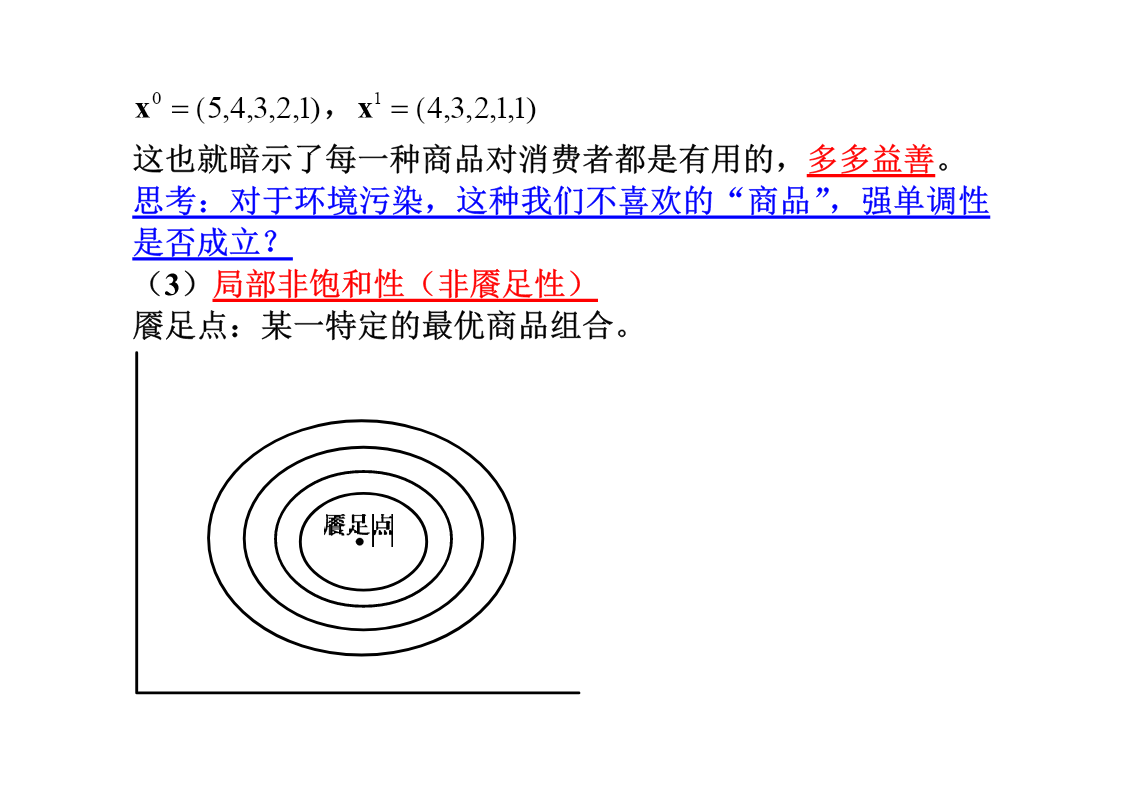
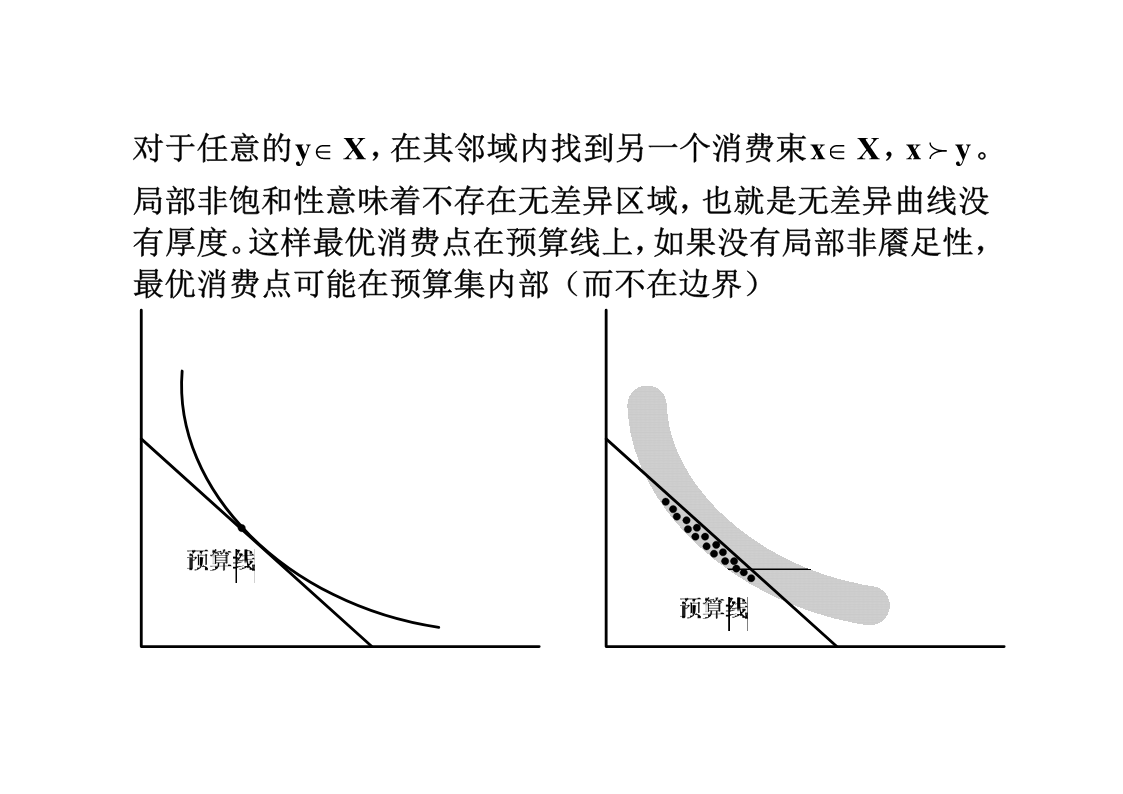
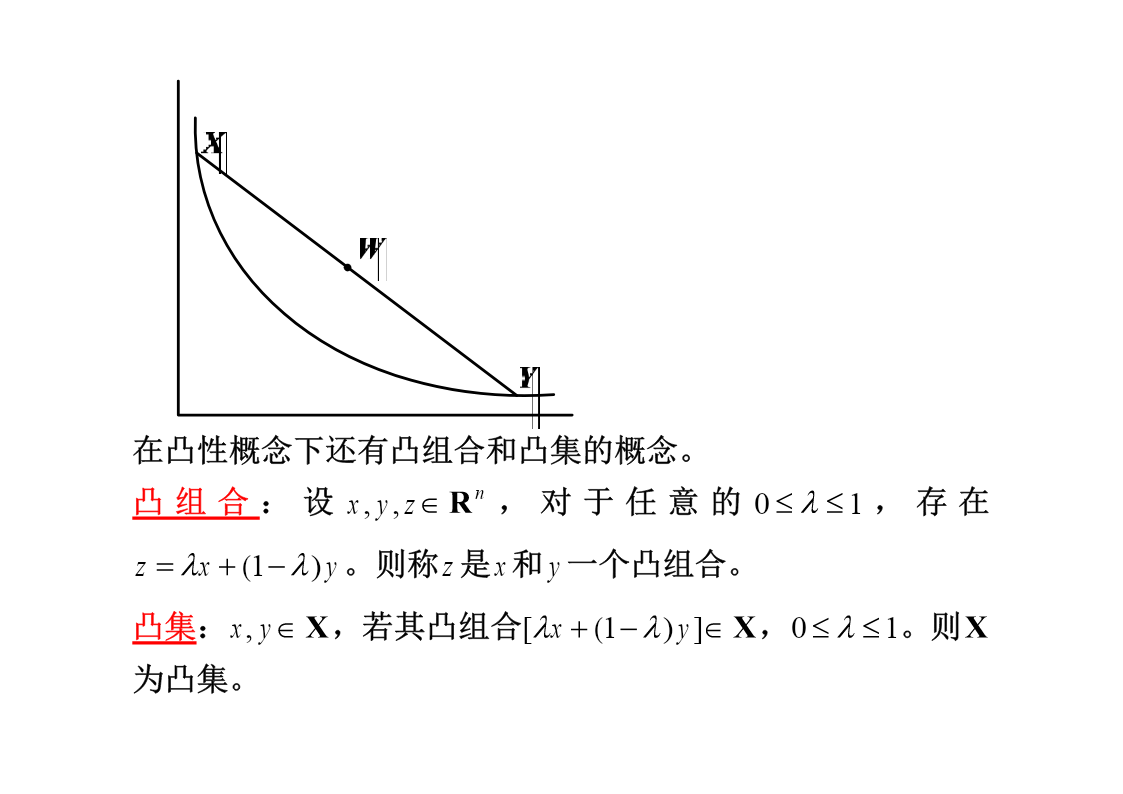
一、理性消费者理性决策的概念：在商品价格和收入约束下，实现最大满足。本章的核心内容就是要介绍消费者的理性选择框架，涉及的概念和使用的工具为：消费束与消费集偏好关系效用函数无差异曲线效用最大化（一）消费束与消费集消费就是购买一系列商品，当然这里的商品可能是实际商品也可以是服务，例如旅游。这一系列被消费的商品组合就成为了一个消费束，用向量表示就是：，其中是x(x1,x2,,xn)xi0对第i种商品的选择数量,i1,2,,n。更一般的，消费是一个广义概念。x(w,l)；x(c1,c2)不同的消费者有不同的消费组合，也就是不同的消费束，所有的消费束的集合就构成了消费集。nnXR，R为n维非负实数向量。nΦXR（非空子集）消费集X是连续的。（消费集是个闭集，包含边界，也就是说所有的消费束都包含在X中，由于消费束有无数多个，填充整个消费集，因此X是连续的。）消费集X是凸集凸集：x,yX，若其凸组合[x(1)y]X，01。则X为凸集。0X（消费者可以选择不消费）（二）偏好关系定义：可选择的消费束上的排序关系。如果只将两个消费束进行比较，称为二元偏好关系，可以用下面一组符号表示：（1）弱偏好关系：xy表示x不次于y，如果yx也成立，则有：（2）无差异：~x~y表示x与y无差异。如果xy但没有yx成立，则有：（3）严格偏好关系：偏好关系是基于序数效用的。一开始经济学家创立了基数效用论，也就是商品消费带来一个实际的效用。但这一假设是不合理的，我们只需要作消费满足多和少的比较，多多少无关紧要，也就是序数效用。偏好关系的公理系统：（1）完备性两个消费束是可以比较的，比较的结果无非三种：xy、yx、x~y（2）自返性一个消费束至少与它本身一样好，即：xX，总有xx（3）传递性如果你喜欢荔枝而不喜欢苹果，但和荔枝相比，你更喜欢樱桃。所以，如果让你从苹果和樱桃中选择，你一定选择樱桃而不是苹果，用符号表示就是：123122313x、x、xX，若xx，xx则xx。上述的三个公理界定了一个理性消费者！为了建立效用函数还需要对偏好做出性质上的假设。（1）连续性对于所有x,yX，则集合{x:xy}和集合{x:xy}都是闭集。也就是说如果x优于y，那么与x非常相似的消费束也优于y，这就保证了突然的偏好逆转不会出现。存在着一条由一组点形成的边界，这条边界在商品空间中把那些消费者偏好的商品组合同不偏好的商品组合划分开来。词典式偏好就会出现逆转情况词典式偏好（字典序偏好关系，lexicographicpreferencerelations）是指某个商品（如商品1）具有优先排序权，只有当商品1的数量相等时，才会就商品2进行排序。表示为若，或者且，则称。x1y1x1y1x2y2xy为什么词典式偏好会出现逆转呢？1令x(1,1)，y(2,1)nnn当时，，当时，，当时，，0<n<1xnynn=1xn~ynnxnyn发生了逆转！（2）强单调性010101对于所有的x和xX，如果xx则xx。x0(5,4,3,2,1)，x1(4,3,2,1,1)这也就暗示了每一种商品对消费者都是有用的，多多益善。思考：对于环境污染，这种我们不喜欢的“商品”，强单调性是否成立？（3）局部非饱和性（非餍足性）餍足点：某一特定的最优商品组合。对于任意的yX，在其邻域内找到另一个消费束xX，xy。局部非饱和性意味着不存在无差异区域，也就是无差异曲线没有厚度。这样最优消费点在预算线上，如果没有局部非餍足性，最优消费点可能在预算集内部（而不在边界）（4）严格凸性10如果两个消费束xx，那么对于所有的[0,1]（闭区间），100都有x(1)xx。也就是多样的消费束要比极端的消费束好？Why？多样的消费降低了相同商品的消费次数，同时增加了其他商品的消费，效用必然增加。思考：请举例说明凹性偏好。在凸性概念下还有凸组合和凸集的概念。凸组合：设x,y,zRn，对于任意的01，存在zx(1)y。则称z是x和y一个凸组合。凸集：x,yX，若其凸组合[x(1)y]X，01。则X为凸集。习题：证明如果偏好关系满足上述公理，若xyz，则xz；二、效用函数（一）效用函数的定义效用满足程度效用函数满足程度与消费集的关系，即：，为消费束。uu(x1,,xn)u(x)x