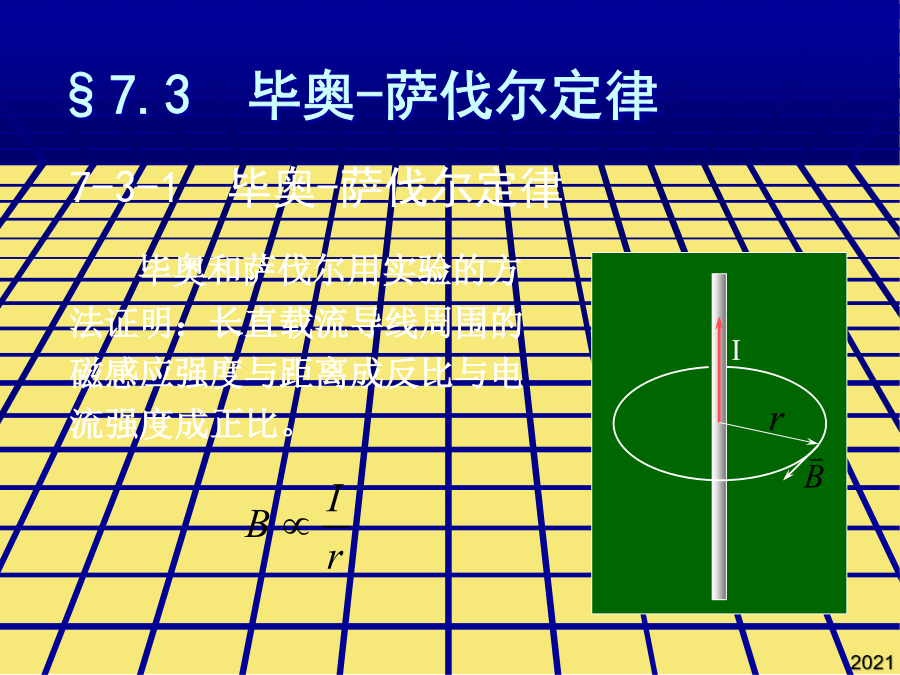
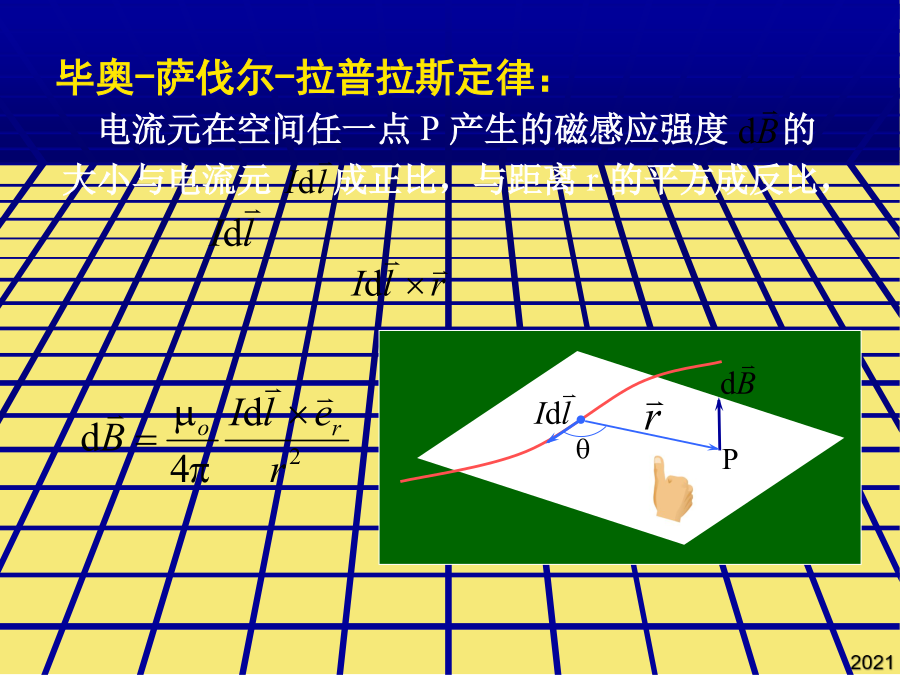
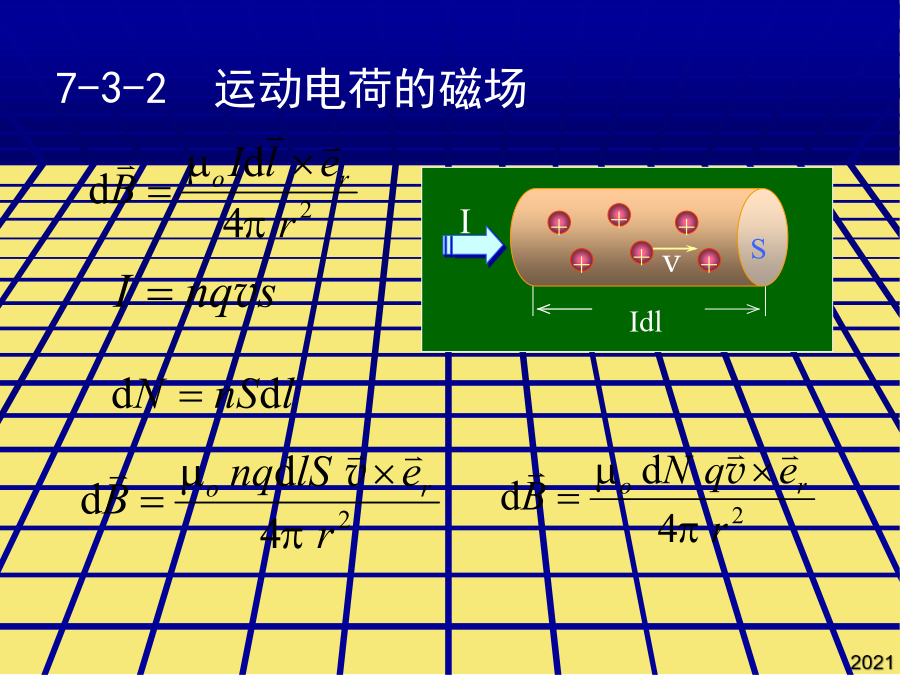
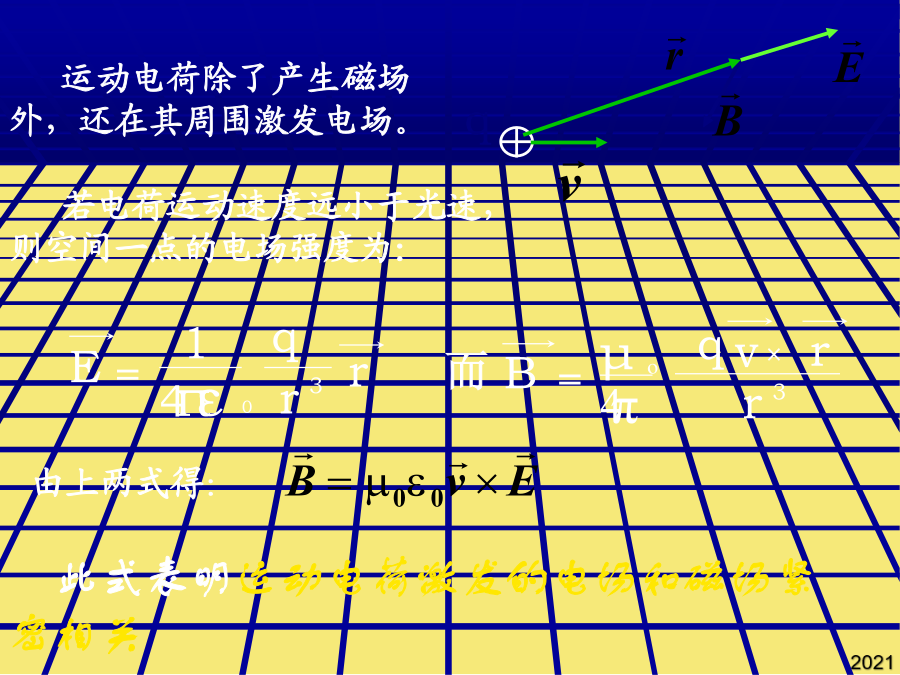
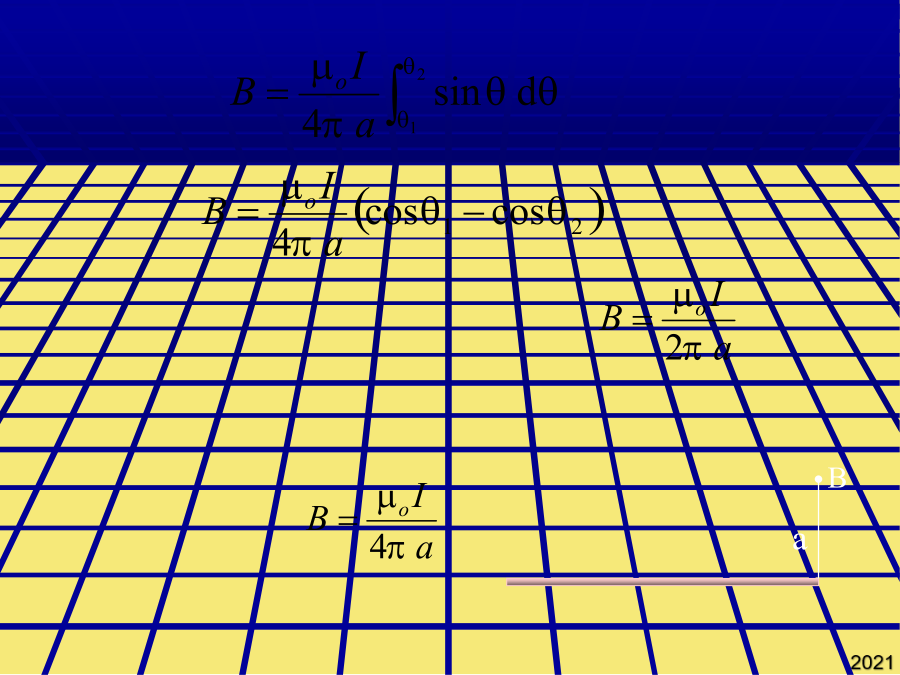
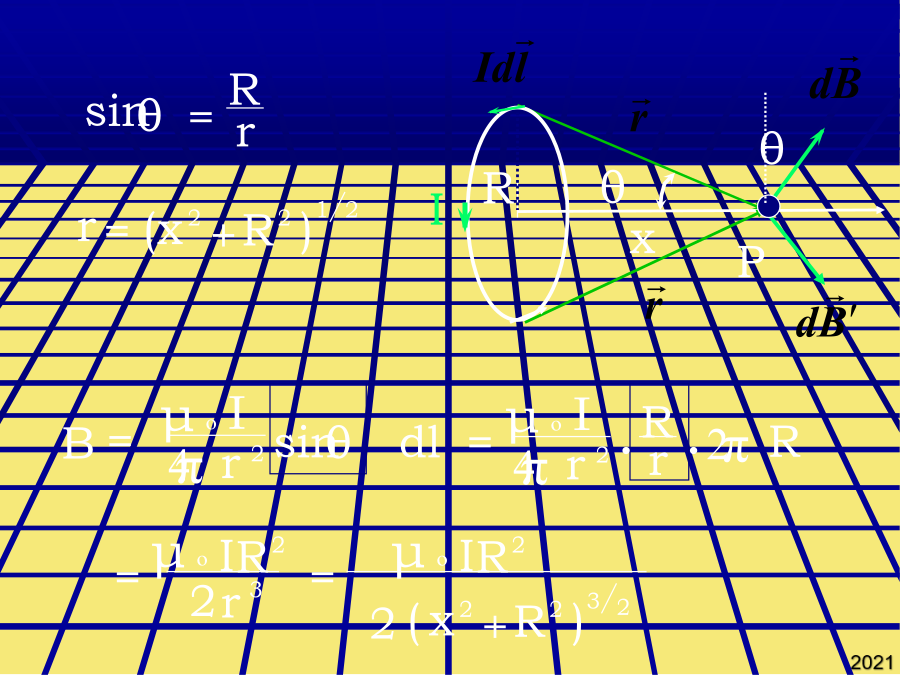
§7.3毕奥-萨伐尔定律毕奥-萨伐尔-拉普拉斯定律：7-3-2运动电荷的磁场运动电荷的磁感应强度公式：运动电荷除了产生磁场外，还在其周围激发电场。7-3-3毕奥-萨伐尔定律的应用1.载流直导线的磁场一载流长直导线，电流强度为I，导线两端到P点的连线与导线的夹角分别为1和2。求距导线为a处P点的磁感应强度。无限长载流导线：1=0,2=Bsin求：圆盘中心处的磁感应强度。在玻尔的氢原子模型中，电子绕原子核运动相当于一个圆电流，具有相应的磁矩（称为轨道磁矩）。7-3-3毕奥-萨伐尔定律的应用如图求Ｏ点的磁感应强度dI在Ｏ点处的磁感应强度为：任意线电流在场点处的磁感应强度B等于构成线电流的所有电流元单独存在时在该点的磁感应强度之矢量和。面积的正法线方向与环电流的流向成右手螺旋关系，其单位矢量用表示。5、有一半径为Ｒ的单匝圆线圈，通以电流Ｉ，若将该导线弯成Ｎ＝２匝的平面线圈，导线长度不变，通以同样的电流，则线圈中心的磁感应强度和线圈的磁矩分别是原来的几倍？dI在Ｏ点处的磁感应强度为：载流密绕直螺线管内部轴线上的磁场5、有一半径为Ｒ的单匝圆线圈，通以电流Ｉ，若将该导线弯成Ｎ＝２匝的平面线圈，导线长度不变，通以同样的电流，则线圈中心的磁感应强度和线圈的磁矩分别是原来的几倍？此式表明运动电荷激发的电场和磁场紧密相关6、如图所示的被折成钝角的长导线中通有20A的电流。设导线中通有电流I。解：两段圆弧在Ｏ点产生的Ｂ１和Ｂ２。运动电荷的磁感应强度公式：载流密绕直螺线管内部轴线上的磁场磁矩：3.载流密绕直螺线管内部轴线上的磁场例1、求以绕轴转动、电量为q的园环中心处的磁感应强度。2、无限多无限长导线，每根通过的电流为Ｉ，组成平面导线排，如图所示。试证：这个：“无限长”电流片上下两边所有各点处的Ｂ的大小相等且有：3、如图半径为Ｒ的带正电且线密度是的半圆，以角速度绕轴Ｏ１Ｏ２匀速旋转。求：（１）、Ｏ点处的Ｂ；（２）、旋转的带电半圆的磁矩。4、如图。求三角形中心点Ｏ处的磁感应强度。5、一个塑料圆盘，半径为R，电荷q均匀分布在表面，圆盘绕通过圆心垂直盘面的轴转动，角速度为ω。求：圆盘中心处的磁感应强度。π4、如图，两个半径为Ｒ的相同金属环在a、b两点相接触（a、b连线为环的直径），并相互垂直放置，电流由a点流入，b端流出，则环中心o点的磁感应强度的大小为：求：A点的磁感应强度。6、如图所示的被折成钝角的长导线中通有20A的电流。如图求Ｏ点的磁感应强度6、如图所示的被折成钝角的长导线中通有20A的电流。若电荷运动速度远小于光速，则空间一点的电场强度为：两段直导线在o产生的Ｂ3和Ｂ4为：磁偶极磁场：圆电流产生的磁场。如图２所示，两个半圆面正交，则Ｏ点处的磁感应强度为多少？此式表明运动电荷激发的电场和磁场紧密相关求距导线为a处P点的磁感应强度。5、有一半径为Ｒ的单匝圆线圈，通以电流Ｉ，若将该导线弯成Ｎ＝２匝的平面线圈，导线长度不变，通以同样的电流，则线圈中心的磁感应强度和线圈的磁矩分别是原来的几倍？5、有一半径为Ｒ的单匝圆线圈，通以电流Ｉ，若将该导线弯成Ｎ＝２匝的平面线圈，导线长度不变，通以同样的电流，则线圈中心的磁感应强度和线圈的磁矩分别是原来的几倍？已知：a,b,I,N例7.在玻尔的氢原子模型中，电子绕原子核运动相当于一个圆电流，具有相应的磁矩（称为轨道磁矩）。求轨道磁矩与轨道角动量之间的关系。根据对称性：By=0磁矩：练习1、一长直导线，沿空间直角坐标Ｏy轴放置，电流沿y轴正方向，在原点o处取一电流元Idl,则该电流元在（a,0,0)点处的磁感应强度的大小为2、有一条载有电流Ｉ的导线弯成如图abcda形状，其中ab,cd是直线段，其它是圆弧，两段圆弧的长度和半径分别为l1,R1,和l2,R2，且两段圆弧共心，求圆心处的Ｂ的大小。3、如图１所示，两个半圆共面，则Ｏ点处的磁感应强度为多少？4、如图，两个半径为Ｒ的相同金属环在a、b两点相接触（a、b连线为环的直径），并相互垂直放置，电流由a点流入，b端流出，则环中心o点的磁感应强度的大小为：5、有一半径为Ｒ的单匝圆线圈，通以电流Ｉ，若将该导线弯成Ｎ＝２匝的平面线圈，导线长度不变，通以同样的电流，则线圈中心的磁感应强度和线圈的磁矩分别是原来的几倍？6、如图所示的被折成钝角的长导线中通有20A的电流。求：A点的磁感应强度。设d=2cm,a=1200π解：9、电流均匀地流过宽度为b的无限长平面导体薄板，电流为I，沿板长方向流动。求：解：（2）通过板的中线并与板面垂直的直线上一点Q处的磁感应强度，Q点到板面的距离为x。B解（１）：如图，dl上的电荷元dq对应的电流强度为：载流密绕直螺线管内部轴线上的磁场毕奥和萨伐尔用实验的方法证明：长直载流导