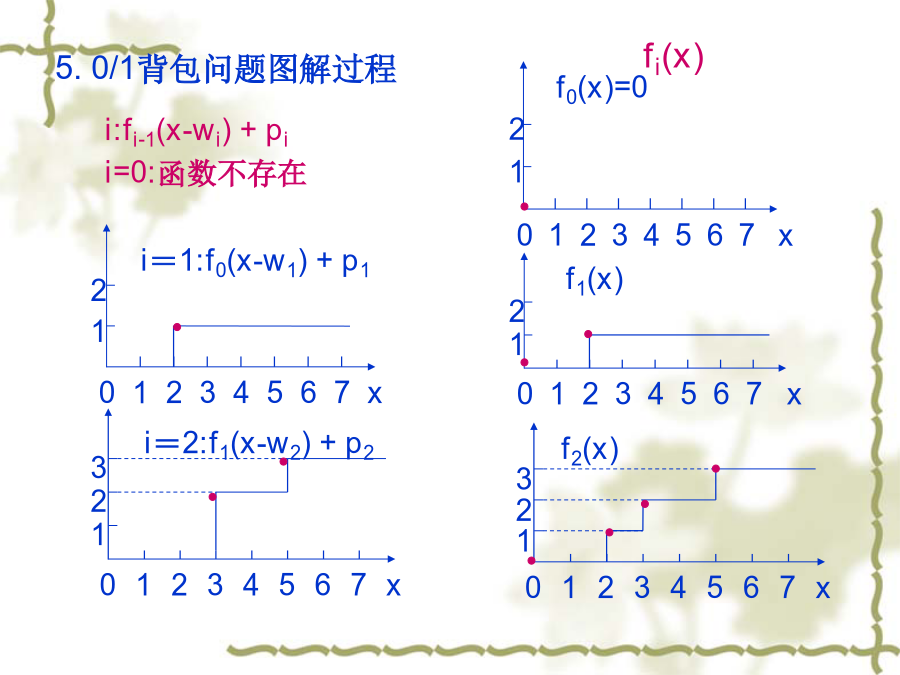
形式化描述：目标函数：约束条件：0/1背包问题：KNAP(1,n,M)0/1背包问题：M=6,N=3,W=(3,3,4),P=(3,3,5)贪心法：p3/w3>p1/w1>p2/w2贪心解∑P=5（0,0,1）最优解是：∑P=6（1,1,0）设y1,y2,…,yn是x1,x2,…,xn的0/1值最优序列。若y1＝0,KNAP(2,n,M)是初始决策产生的状态。则y2,…,yn相对于KNAP(2,n,M)将构成一个最优序列。否则，y1,y2,…,yn将不是KNAP(1,n,M)的最优解若y1＝1,KNAP(2,n,M－w1)是初始决策产生的状态。则y2,…,yn相对于KNAP(2,n,M－w1)将构成一个最优序列。否则，设存在另一0/1序列z1,z2,…,zn,使得且则序列y1,z2,…,zn将是一个对于KNAP(1,n,M)具有更大效益值的序列。故，最优性原理成立3从前向后求解的递推关系式记fj(X)是KNAP(1,j,X)的最优解，则fn(M)是KNAP(1,n,M)的最优解对于fn(M)有：fn(M)=max{fn-1(M),fn-1(M-wn)+pn}对于任意的fi(X)，i＞0,有fi(X)=max{fi-1(X),fi-1(X-wi)+pi}递推过程：★初始值0X≥0f0（X）=－∞X＜0★f1(X)=max{f0(X),f0(X-W1)+P1}求出所有可能的X对应的fi值★fi(X)=max{fi-1(X),fi-1(X-Wi)+Pi}★最后求fn(M)=KNAP(1,n,M)4例用动态规划法求解0/1背包问题n=3,(w1,w2,w3)=(2,3,4),(p1,p2,p3)=(1,2,5)，M=6递推计算过程－∞X＜0f0(X)=0X≥0－∞X＜0max{0,－∞+1}=00≤X＜2max{0,0+1}=1X≥2－∞X＜000≤X＜212≤X＜3max{1,0+2}=23≤X＜5max{1,1+2}=3X≥5f3(M)=max{3,1+5}=6解向量的推导f3(M)=6f2(M)<>65.0/1背包问题图解过程16.序偶表示法记fi(X)的序偶集合为Si={(Pj,Wj)|Wj是fi曲线中使得fi产生一次阶跃的X值，0≤j＜r}即Pj=fi(Wj)●(P0,W0)=(0,0)●图中有r个阶跃值,对应r个(Pj,Wj)序偶,1≤j≤r●图中若Wj＜Wj+1,则Pj＜Pj+1，0≤j＜r●图中若Wj≤X＜Wj+1，fi(X)=fi(Wj)●图中若X≥Wr，fi(X)=fi(Wr)●Si的构造记是fi-1(X-wi)+pi的所有序偶的集合，则其中，Si-1是fi-1的所有序偶的集合Si的构造：由Si-1和按照支配规则合并而成。支配规则：如果Si-1和之一有序偶(Pj,Wj),另一有(Pk,Wk)，且有Wj≥Wk,Pj≤Pk，则序偶(Pj,Wj)将被舍弃。（即取最大值规则）。初始序偶集合S0={(0,0)}例2例1的序偶表示法S0={(0,0)}={(1,2)}S1={(0,0),(1,2)}={(2,3),(3,5)}S2={(0,0),(1,2),(2,3),(3,5)}={(5,4),(6,6),(7,7)}S3={(0,0),(1,2),(2,3),(5,4),(6,6),(7,7)}注：序偶(3,5)被(5,4)“支配”而删除KNAP(1,n,M)问题的解★Sn是KNAP(1,n,X)在0≤X≤M各种取值下的最优解★KNAP(1,n,M)的最优解由Sn的最后一对有效序偶给出。xi的推导xn:设Sn的最后一对有效序偶是(Pl,Wl)，则(Pl,Wl)或者是Sn－1的最末一对序偶，或者是(Pj+pn,Wj+wn)，其中(Pj,Wj)∈Sn－1且Wj是Sn－1中满足Wj+wn≤M的最大值。●若(Pl,Wl)∈Sn－1，则Xn＝0；否则，●(Pl－pn,Wl-wn)∈Sn－1，Xn＝1xn-1:若xn=0，则判断(Pl,Wl)∈Sn－2？，以确定Xn-1的值若xn=1，则依据(Pl－pn,Wl-wn)∈Sn－2？，以判断Xn-1的值xn-2,…,x1将依次推导得出例2的解向量推导S0={(0,0)}S1={(0,0),(1,2)}S2={(0,0),(1,2),(2,3),(3,5)}S3={(0,0),(1,2),(2,3),(5,4),(6,6)}M=6，f3(6)由S3中的序偶(6,6)给出。1)∵(6,6)S2∴x3=12)∵(6-p3,6-w3)=(1,2)∈S2且(1,2)∈S1∴x2=03)∵