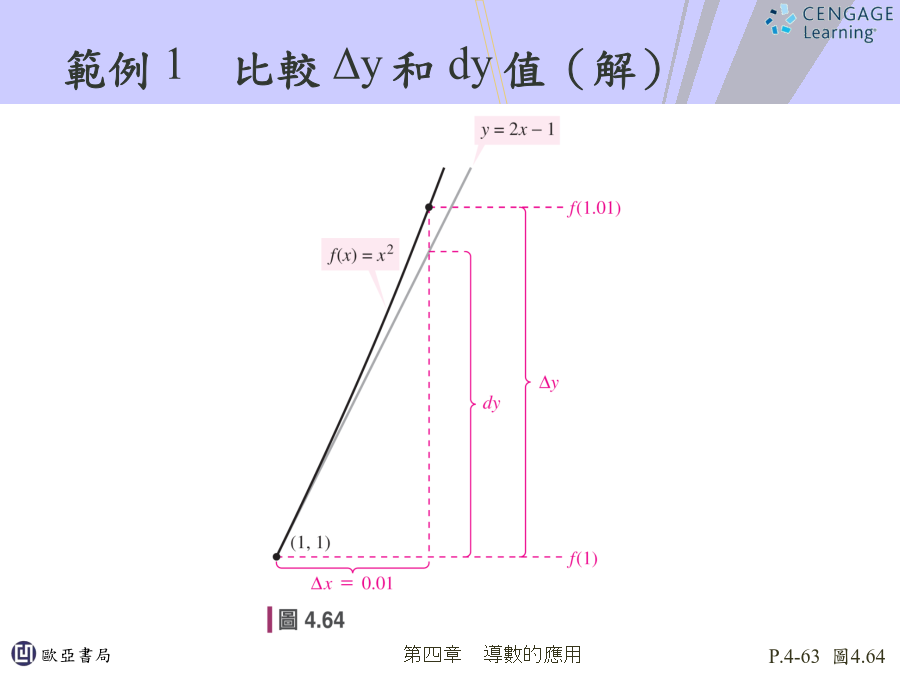
4.8微分量與邊際分析在3.1節中導數的定義為Δy/Δx比值的極限，此極限自然地保留比值的形式，所以y對x的導數可記為此處不要將dy/dx看成兩個不同變化量dy與dx的比值。本節將賦予dy和dx特殊意義，使得在dx≠0時，其比值等於y對x的導數。在本節的dx為任意非零的實數，可是在實例應用中，令dx為很接近零的值，並以dx＝Δx來表示。微分量微分量微分量範例1比較Δy和dy值範例1比較Δy和dy值（解）範例1比較Δy和dy值（解）範例1比較Δy和dy值（解）檢查站1微分量切線估算法dyΔy,dx0的正確性源自於導數的定義；也就是極限的存在，當Δx越來越接近零，則f(x)越來越接近兩變化量的比值。所以將Δx代入dx和f(x)dx代入dy可得Δydy。微分量在經濟學上用於估算收入、成本和利潤的變化量。假設R＝f(x)為銷售x單位產品的總收入，銷售量每增加1單位，x的變化量為Δx＝1，則R的變化量為也就是，微分量dR可用來估算公司銷售量每增加1單位所產生的收入變化量；同理，微分量dC與dP可用來估算公司銷售量每增加1單位所產生的成本和利潤的變化量。範例2使用邊際分析首先求邊際收入。因為需求為p＝400－x，則收入為R=xp收入的公式=x(400－x)以p＝400－x代入=400x－x2相乘接著計算邊際收入dR/dx乘冪法範例2使用邊際分析（解）範例2使用邊際分析（解）檢查站2範例3使用邊際分析邊際利潤為當x＝50和dx＝Δx＝1時的微分量為範例3使用邊際分析（解）範例3使用邊際分析（解）檢查站3微分量的公式微分量的公式範例4求微分量檢查站4總結(4.8節)