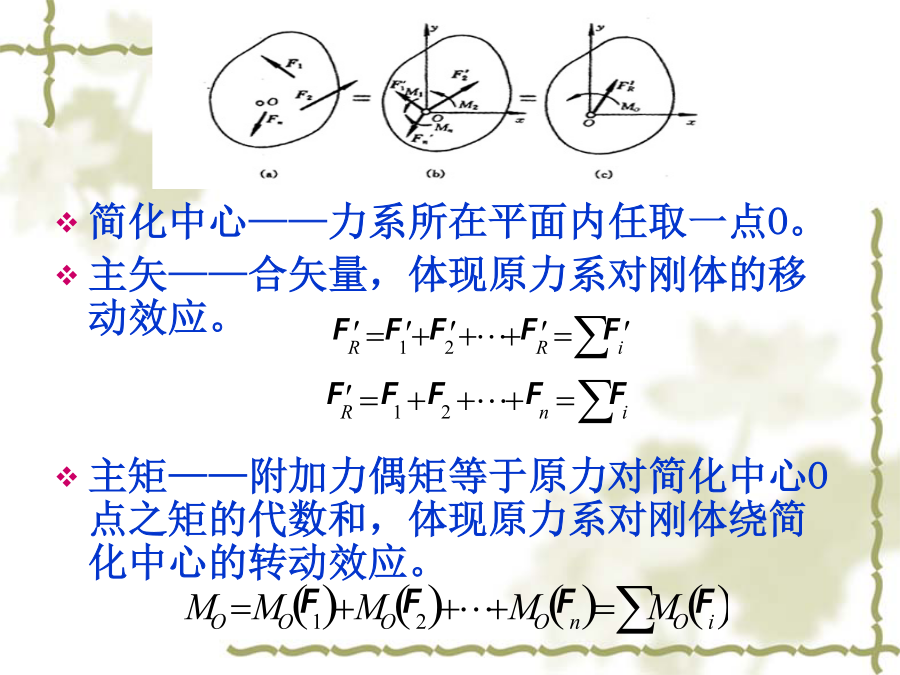
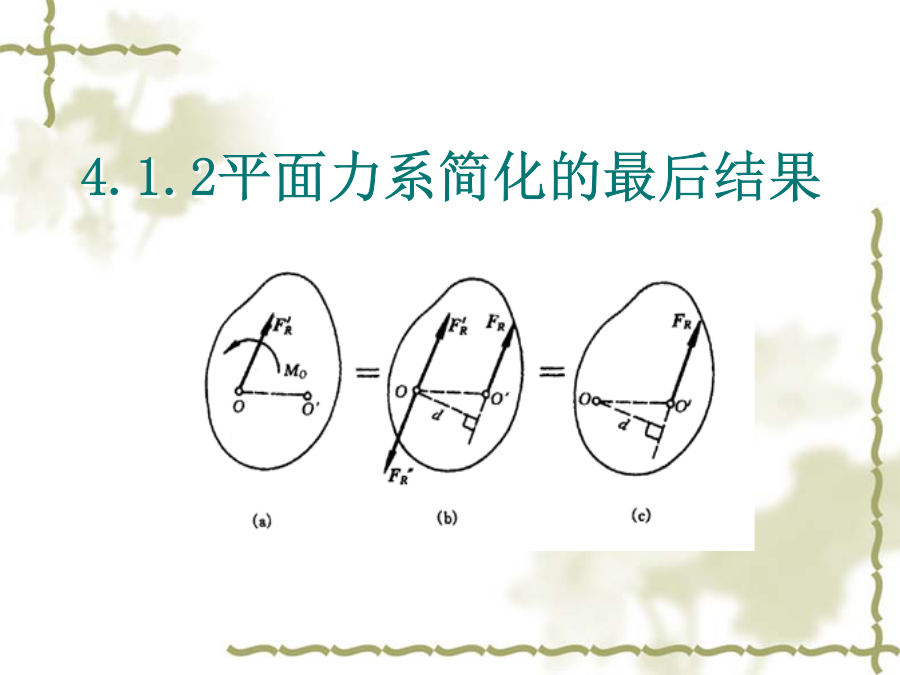
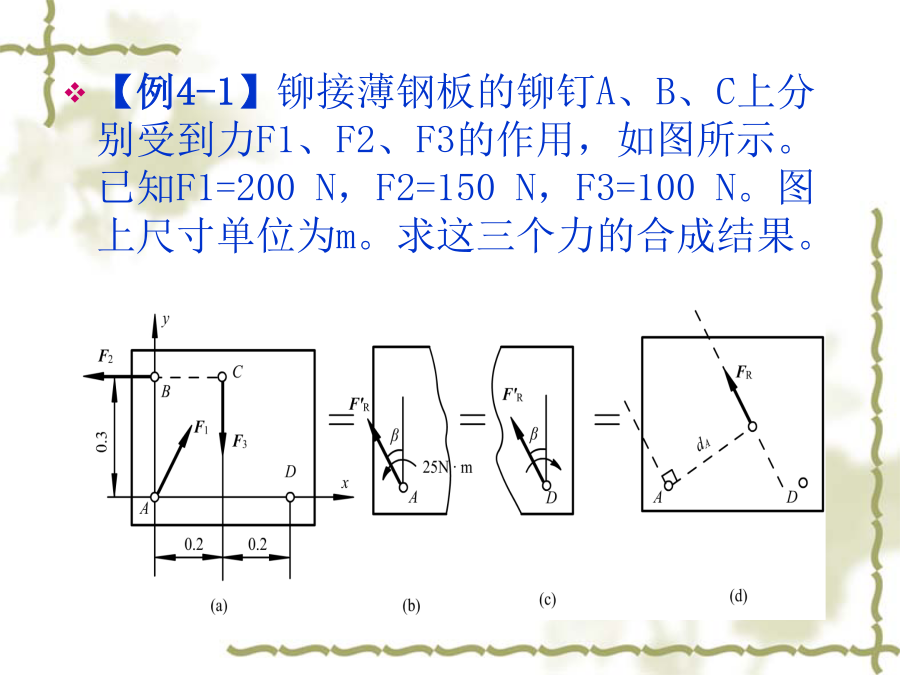
4.1平面力系的简化4.1.1平面力系向一点的简化简化中心——力系所在平面内任取一点O。主矢——合矢量，体现原力系对刚体的移动效应。主矩——附加力偶矩等于原力对简化中心O点之矩的代数和，体现原力系对刚体绕简化中心的转动效应。综上所述可知，平面力系向一点（简化中心）简化的一般结果是一个力和一个力偶：这个力作用于简化中心，称为原力系的主矢，它等于原力系中所有各力的矢量和；这个力偶的矩称为原力系对简化中心的主矩，它等于原力系中所有各力对于简化中心力矩的代数和。力系的主矢与简化中心的位置无关。主矩一般随简化中心的位置不同而改变。4.1.2平面力系简化的最后结果（1）若主矢≠0，则不论主矩Ｍo是否等于零，原力系简化的最后结果为一个力，此力称为平面力系的合力。这时又可分为两种情况:1、当Ｍo＝0时，则作用于简化中心的力就是原力系的合力ＦR。此时简化中心O恰好选在了平面力系合力的作用线上。2、当Ｍo≠0时，原力系简化为作用线通过简化中心的一个力和一个矩为Ｍo的力偶，如图（a）所示，根据力的平移定理的逆定理，可以把此力与力偶进一步合成为一合力ＦR。合力FR作用线与简化中心O的垂直距离为：合力ＦR的作用线在简化中心O的哪一侧，应根据主矩Ｍo的转向决定，合力FR对简化中心之矩与主矩的转向应一致。（2）若主矢＝0，主矩Ｍo≠0，则原力系简化的最后结果为一个力偶，此力偶称为平面力系的合力偶，其力偶矩等于主矩，即M=Mo=∑Mo(Fi)。此时主矩与简化中心的位置无关，是一常量，亦即原力系向任意点简化的结果都是其矩为Mo的力偶，这也反映了力偶可在作用面内任意移转这一特性。（3）若主矢＝0，主矩Mo＝0，这说明原力系合成为零力系，则原力系平衡，这种情况将在下一章重点讨论。【例4-1】铆接薄钢板的铆钉A、B、C上分别受到力F1、F2、F3的作用，如图所示。已知F1=200N，F2=150N，F3=100N。图上尺寸单位为m。求这三个力的合成结果。【分析】(1)将力系向A点简化，其主矢为，主矩为主矢在x、y轴上的投影为主矢大小：主矢方向：主矩：（2）因为，，所以原力系还可以进一步简化为一个合力FR，其大小与方向和主矢相同，即合力的作用线位置到A点的垂直距离因为为逆时针，故最终合力的作用线在A点的右边，如图所示。【例4-2】胶带运输机传动滚筒的半径R=0.325m，由驱动装置传来的力偶矩M=4.65kN·m，紧边皮带张力FT1=19kN，松边皮带张力FT2=4.7kN，皮带包角为210°，坐标位置如图（a）所示，试将此力系向点O简化。【分析】将力系向O点简化（1）求主矢主矢在x、y轴上的投影为主矢大小：主矢方向：（2）求主矩由于主矩为零，故力系的合力即等于主矢，且合力的作用线通过简化中心O，如图所示。4.2平面力系的平衡方程及其应用4.2.1平面力系的平衡条件与平衡方程平面力系平衡的充分与必要条件是力系的主矢和力系对任意点的主矩都等于零。即上面的平衡条件可用下面的解析式表示：4.2.2平面力系平衡方程的应用【例4-3】简易起重机的水平梁AB，A端以铰链固定，B端用拉杆BC拉住，如图所示。水平梁AB自重G=4kN，载荷FP=10kN，尺寸单位为m，BC杆自重不计，求拉杆BC所受的拉力和铰链A的约束反力。【分析】（1）选取梁AB(包括重物)为研究对象，画其受力图。梁AB除受到主动力G、FP作用外，还有未知约束反力，包括拉杆的拉力FT和铰链A的约束反力FAx、FAy。因杆BC为二力杆，故拉力FT沿BC中心线方向。这些力的作用线可近似认为分布在同一平面内,如图（b）所示。（2）选取坐标系Axy，矩心为A点，如图（b）所示。（3）各个力向x,y轴投影,并对A点取力矩建立平衡方程。将已知量代入③式得FT=17.3kN将FT代入①、②式得计算结果FAx、FAy和FT皆为正值,表明这些力的实际指向与图示假设的指向相同。讨论：计算结果正确与否，可任意列一个上边未用过的平衡方程进行校核。例如：选取D点为矩心故原计算结果正确。【分析】（1）以起重机为研究对象，画出受力图。起重机上作用有主动力W和FP；止推轴承A有轴向反力FAy和径向反力FAx；径向轴承B只有一个垂直于转轴的径向反力FB，其指向假设向右，如图（b）所示。（2）选取坐标系Axy，如图（b）所示，列平衡方程并求解：平面任意力系的平衡方程还有下列两种形式：1）二矩式：其中，投影轴x不能与矩心A、B两点的连线相垂直。这是因为平面任意力系满足，则表明该力系不可能简化为一力偶，只可能是作用线通过A点的一合力或平衡。若力系又满足,同理可以断定，该力系简化结果只可能为一作用线通过A、B两点的一个合力（如图所示）