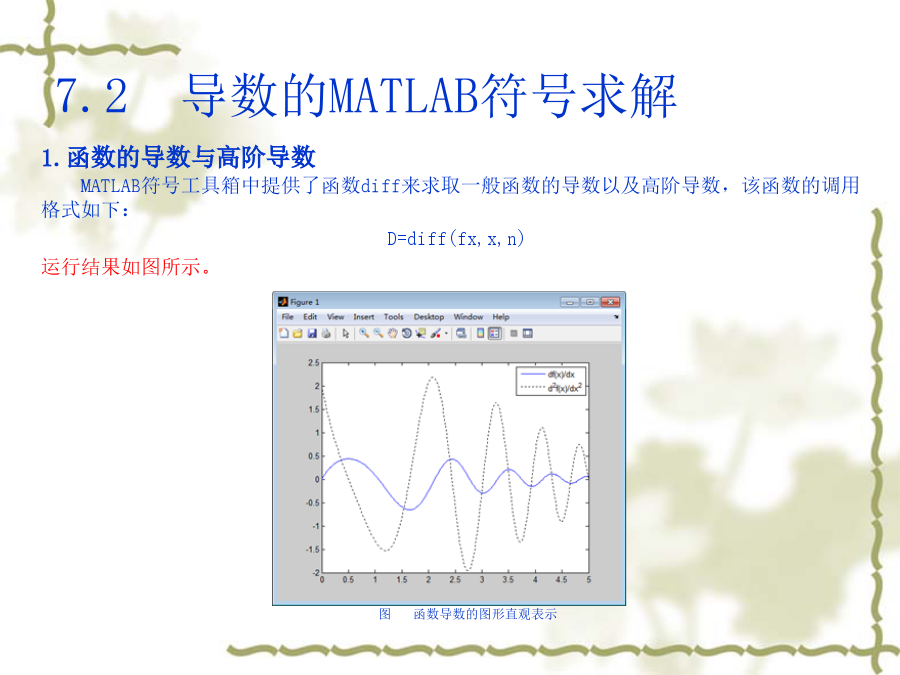
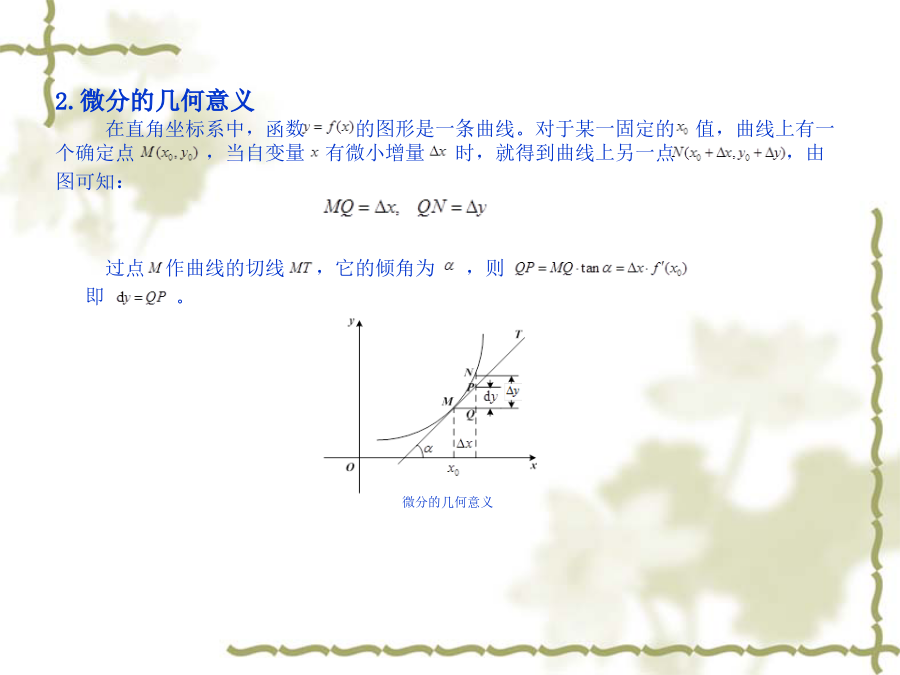
Outline7.1导数概念2.导数的几何意义函数在点处的导数在几何上表示曲线在点处的切线的斜率，即其中是切线的倾角。如果函数在点处的导数为无穷大，这时曲线的割线以垂直于轴的直线为极限位置，即曲线在点处具有垂直于轴的切线。7.2导数的MATLAB符号求解2.隐函数的导数方程表示一个函数，因为当自变量在内取值时，变量有确定的值与之对应。例如，当时，；当时，，等等，这样的函数称为隐函数。一般的，如果变量和满足一个方程，在一定条件下，当取某区间内的任一值时，相应的总有满足这方程的唯一的值存在，那么就说方程在该区间内确定了一个隐函数。隐函数求导的一般采用如下步骤：方程两边同时对求导，这里应注意；整理求得的表达式，即为隐函数的导数。3.由参数方程所确定的函数的导数若已知参数方程，则可以由如下递推公式求出：7.3函数的微分2.微分的几何意义在直角坐标系中，函数的图形是一条曲线。对于某一固定的值，曲线上有一个确定点，当自变量有微小增量时，就得到曲线上另一点，由图可知：过点作曲线的切线，它的倾角为，则即。微分的几何意义7.4微分中值定理2.拉格朗日中值定理罗尔定理中这个条件是相当特殊的，它使罗尔定理的应用受到限制。如果把这个条件取消，但仍保留其余两个条件，并相应的改变结论，那么就得到微分学中十分重要的拉格朗日中值定理。如果函数满足：在闭区间上连续；在开区间内可导；那么在内至少有一点，使得成立。关于拉格朗日中值定理的证明此处从略，这里仅介绍该定理的几何意义，如图所示。由于上式可以改写为且为弦的斜率，而为曲线在点处的切线的斜率。因此拉格朗日中值定理的几何意义是：如果连续曲线的弧上除端点外处处具有不垂直于轴的切线，那么该弧上至少有一点，使曲线在点处的切线平行于弦。而且易知，罗尔定理是拉格朗日中值定理的一种特殊情形。拉格朗日中值定理图形直观表示3.柯西中值定理前面已经指出，如果连续曲线弧上除端点外处处具有不垂直于横轴的切线，那么这段弧上至少有一点，使曲线在点处的切线平行于弦。设由参数方程表示，如图所示。其中为参数，那么曲线上点处的切线的斜率为弦的斜率为假定点对应于参数，那么曲线上点处的切线平行于弦，可表示为柯西中值定理图形直观表示7.5洛必达法则2.型洛必达法则下面我们着重介绍型的洛必达法则，事实上，这种形式的洛必达法则在实际中用的较多，而且型也可以由型变换得到，关于该种类型的洛必达法则同样有以下两个定理：设函数与满足：当时，函数与都趋于零；在点的某去心邻域内，与都存在且；存在（或为无穷大），那么7.6泰勒公式7.7函数的单调性与曲线的凹凸性2.曲线的凹凸性与拐点我们从几何上可以看到，在有的曲线弧上，如果任取两点，则联结这两点间的弦总位于这两点间的弧段的上方，而有的曲线弧，则正好相反。曲线的这种性质就是曲线的凹凸性。因此曲线的凹凸性可以用联结曲线弧上任意两点的弦的中点与曲线弧上相应点（即具有相同横坐标的点）的位置关系来描述，下面给出曲线凹凸性的定义。设在区间上连续，如果对上任意两点，恒有那么称在上的图形是（向上）凹的（或凹弧）；如果恒有那么称在上的图形是（向上）凸的（或凸弧）。如果函数在区间内具有二阶导数，那么可以利用二阶导数的符号来判定曲线的凹凸性，这就是下面的曲线凹凸性的判定定理。这里仅就为闭区间的情形来叙述曲线凹凸性的判定定理，当不是闭区间时，定理类同。设在区间上连续，在内具有一阶和二阶导数，那么若在内，则在上的图形是凹的；若在内，则在上的图形是凸的。一般的，设在区间上连续，是的内点，如果曲线在经过点时，曲线的凹凸性改变了，那么就称点为曲线的拐点。7.8函数的极值与最值2.最大值最小值问题在求函数的最大值（或最小值）时，特别值得指出的是下述情：在一个区间（有限或无限、开或闭）内可导且只有一个驻点，并且这个驻点是函数的极值点，那么，当是极大值时，就是在该区间上的最大值；当是极小值时，就是在该区间上的最小值。7.9曲线的渐近线7.10曲率2.曲率及其计算公式在实际中，我们通常使用曲率来描述曲线的弯曲程度。设曲线是光滑的，在曲线上选定一点作为度量弧的基点。设曲线上点对应于弧，在点处切线的倾角为（这里假定曲线所在的平面上已设定了坐标系），曲线上另外一点对应于弧，在点处切线的倾角为，如图所示，那么，弧段的长度为，当动点从移动到时切线转过的角度为。我们用比值，即单位弧段上切线转过的角度的大小来表达弧段的平均弯曲程度，把该比值叫做弧段的平均曲率，并记作，即当时（即时），上述平均曲率的极限叫做曲线在点处的曲率，记作，即曲率推导示意图对于直线来说，切线与直线本