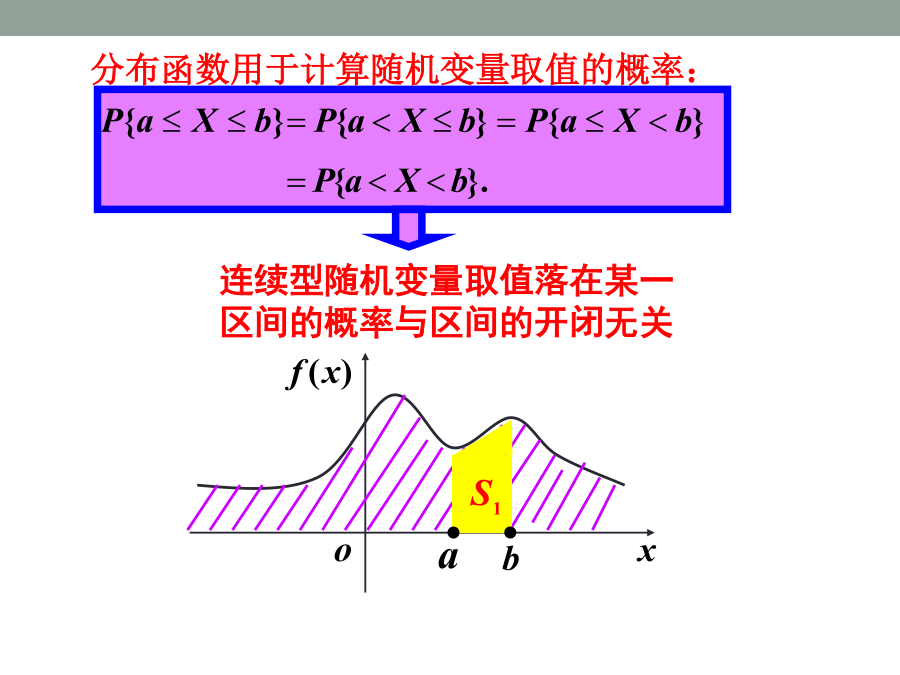
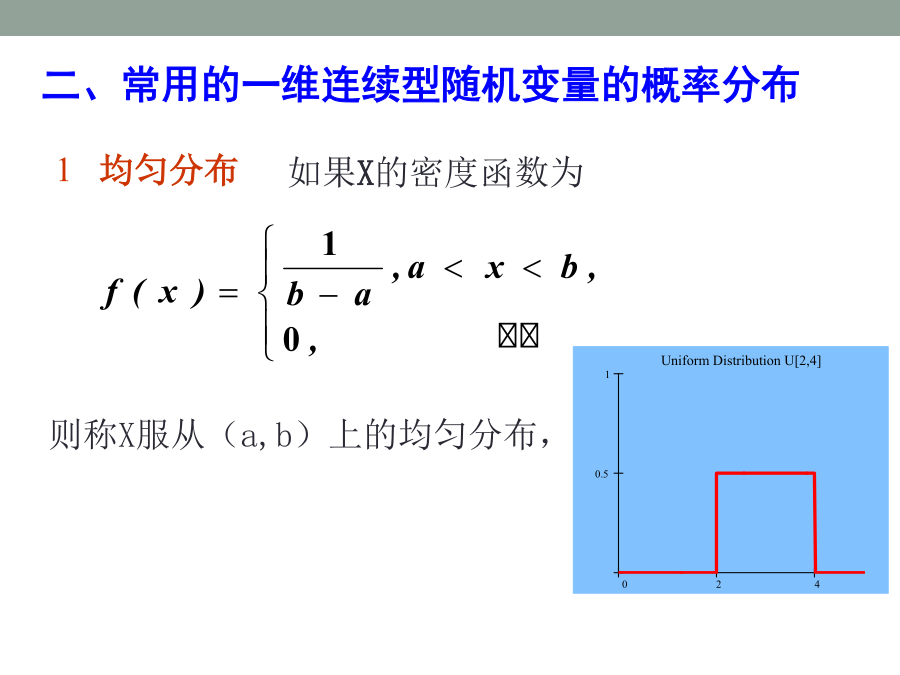
一、一维连续型随机变量及其分布密度概率密度f(x)的性质：若X是连续型随机变量，{X=a}是不可能事件，则有对于连续型随机变量X，其分布函数分布函数用于计算随机变量取值的概率：则称X服从（a,b）上的均匀分布，记为XU(a,b)均匀分布的意义分布函数例2某公共汽车站从上午7时起，每15分钟来一班车，即7:00，7:15，7:30,7:45等时刻有汽车到达此站，如果乘客到达此站时间X是7:00到7:30之间的均匀随机变量,试求他候车时间少于5分钟的概率.为使候车时间X少于5分钟，乘客必须在7:10到7:15之间，或在7:25到7:30之间到达车站.例3设随机变量X在[2,5]上服从均匀分布,现对X进行三次独立观测,试求至少有两次观测值大于3的概率.因而有则称X服从参数为的指数分布.记作XE()某些元件或设备的寿命服从指数分布.例如无线电元件的寿命、电力设备的寿命、动物的寿命等都服从指数分布.例4.设随机变量X服从的指数分布，试求：3正态分布正态分布是应用最广泛的一种连续型分布.正态分布的分布密度及分布函数图像：（4）参数确定曲线的中心位置，影响曲线的形状.曲线在处有拐点。当时，称随机变量X服从标准正态分布，记为XN(0,1)其密度函数为若XN(0,1),则其分布函数为一般正态分布与标准正态分布的关系：标准正态分布函数的函数值表的用法：正态分布是最常见最重要的一种分布,例如测量误差,人的生理特征尺寸如身高、体重等;正常情况下生产的产品尺寸:直径、长度、重量、高度等都近似服从正态分布.例5公共汽车车门的高度是按男子与车门顶头碰头机会在0.01以下来设计的.设男子身高X～N(170,62),问车门高度应如何确定?因为X～N(170,62),二项分布的正态近似例6将一枚硬币抛掷10000次，出现正面5800次，认为这枚硬币不均匀是否合理?试说明理由.=1-Φ(16)