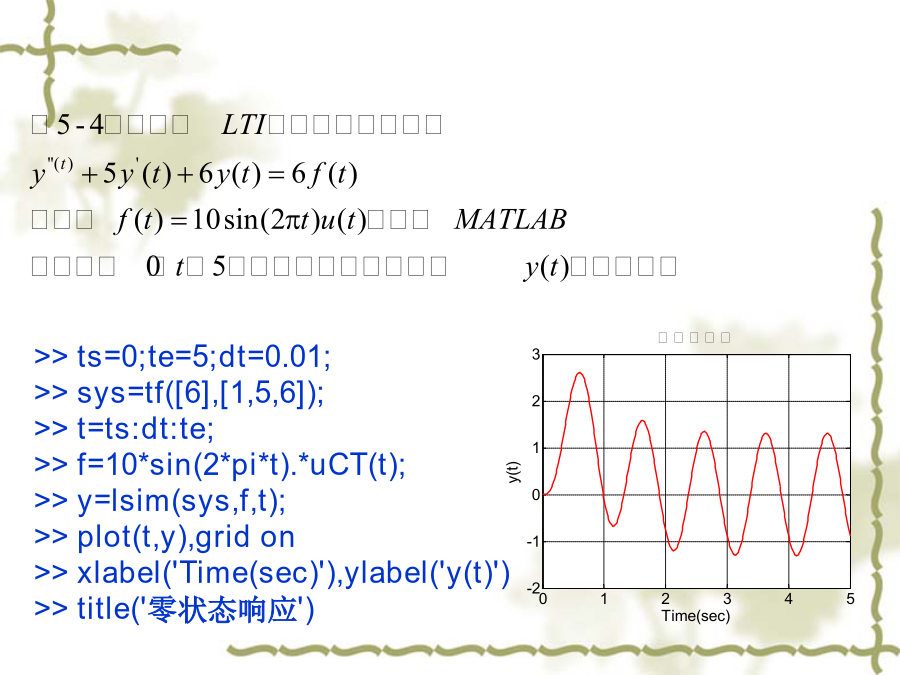
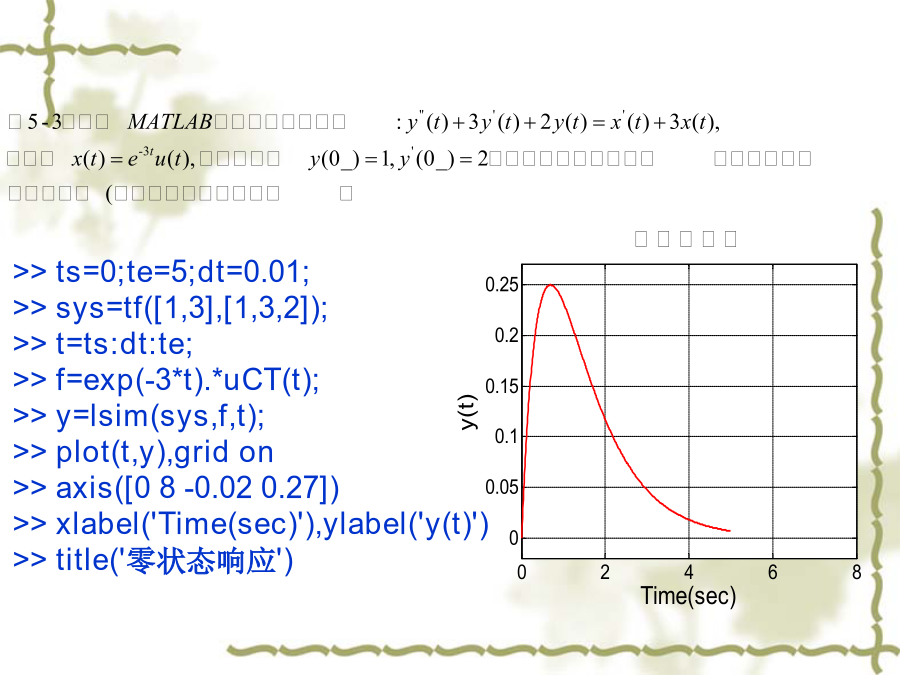
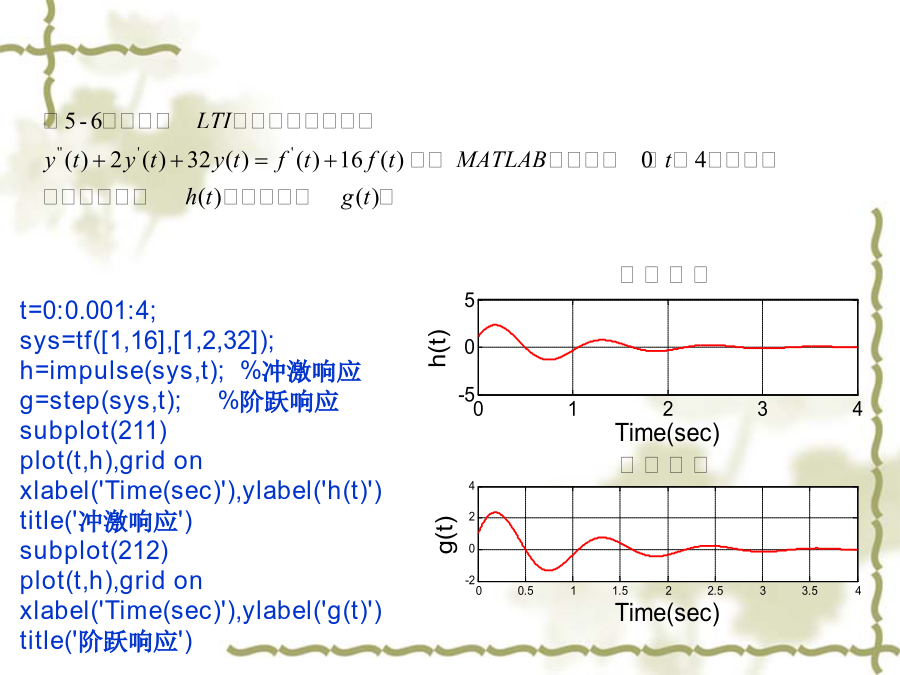
>>eq='D3y+2*D2y+Dy=0';>>cond='y(0)=1,Dy(0)=1,D2y(0)=2';>>ans=dsolve(eq,cond);>>simplify(ans)%化简eq1='D3y+4*D2y+8*Dy=3*Dx+8*x';eq2='x=Heaviside(t)';cond='y(-0.01)=0,Dy(-0.01)=0,D2y(-0.01)=0';ans=dsolve(eq1,eq2,cond);simplify(ans.y)解：求的零输入响应和零状态响应后，完全响应则为二者之和>>eq='D2y+3*Dy+2*y=0';%齐次解求零输入相应>>cond='y(0)=1,Dy(0)=2';>>yzi=dsolve(eq,cond);yzi=simplify(yzi)yzi=-3*exp(-2*t)+4*exp(-t)>>eq1='D2y+3*Dy+2*y=Dx+3*x';%零状态响应求解>>eq2='x=exp(-3*t)*heaviside(t)';>>cond='y(-0.001)=0,Dy(-0.001)=0';%起始条件>>yzs=dsolve(eq1,eq2,cond);yzs=simplify(yzs.y)yzi=heaviside(t)*(-exp(-2*t)+exp(-t))>>yt=simplify(yzi+yzs)%完全响应yt=-3*exp(-2*t)+4*exp(-t)-exp(-2*t)*heaviside(t)+exp(-t)*heaviside(t)利用符号求解出零输入响应、零状态响应及完全响应及完全响应后，可利用ezplot命令绘出他的波形，以便观察。第五章连续时间LTI系统的时域分析>>ts=0;te=5;dt=0.01;>>sys=tf([6],[1,5,6]);>>t=ts:dt:te;>>f=10*sin(2*pi*t).*uCT(t);>>y=lsim(sys,f,t);>>plot(t,y),gridon>>xlabel('Time(sec)'),ylabel('y(t)')>>title('零状态响应')>>ts=0;te=5;dt=0.01;>>sys=tf([1,3],[1,3,2]);>>t=ts:dt:te;>>f=exp(-3*t).*uCT(t);>>y=lsim(sys,f,t);>>plot(t,y),gridon>>axis([08-0.020.27])>>xlabel('Time(sec)'),ylabel('y(t)')>>title('零状态响应')5.3连续时间系统冲激响应和阶跃响应的求解t=0:0.001:4;sys=tf([1,16],[1,2,32]);h=impulse(sys,t);%冲激响应g=step(sys,t);%阶跃响应subplot(211)plot(t,h),gridonxlabel('Time(sec)'),ylabel('h(t)')title('冲激响应')subplot(212)plot(t,h),gridonxlabel('Time(sec)'),ylabel('g(t)')title('阶跃响应')5.4利用卷积积分法求系统的零状态响应dt=0.01;t1=0:dt:4;f1=exp(-2*t1);t2=t1sys=tf([1,16],[1,2,32]);f2=impulse(sys,t2);[t,f]=ctsconv(f1,f2,t1,t2,dt);如果用前面学习的lsim函数来求解，则6.1周期信号的傅里叶级数例6-1周期方波信号如图6-1所示，试求出该信号的傅里叶级数，利用MATLAB编程实现其各次谐波的叠加，并验收其收敛性。t=-1:0.001:1;omega=2*pi;y=square(2*pi*t,50);plot(t,y),gridonxlabel('t'),ylabel('周期方波信号')axis([-11-1.51.5])n_max=[1351147];N=length(n_max);fork=1:Nn=1:2:n_max(k);b=4./(pi*n);x=b*sin(omega*n'*t);figureplot(t,y);holdonplot(t,x)holdoffxlabel('t'),ylabel('部分和的波形')axis([-11-1.51.5]),gridontitle(['最大谐波数=',num2str(n_max(k))])end6.2周期信号的频谱分析n=-30:30;tao=1;T=10;w1=2*pi/T;x=n