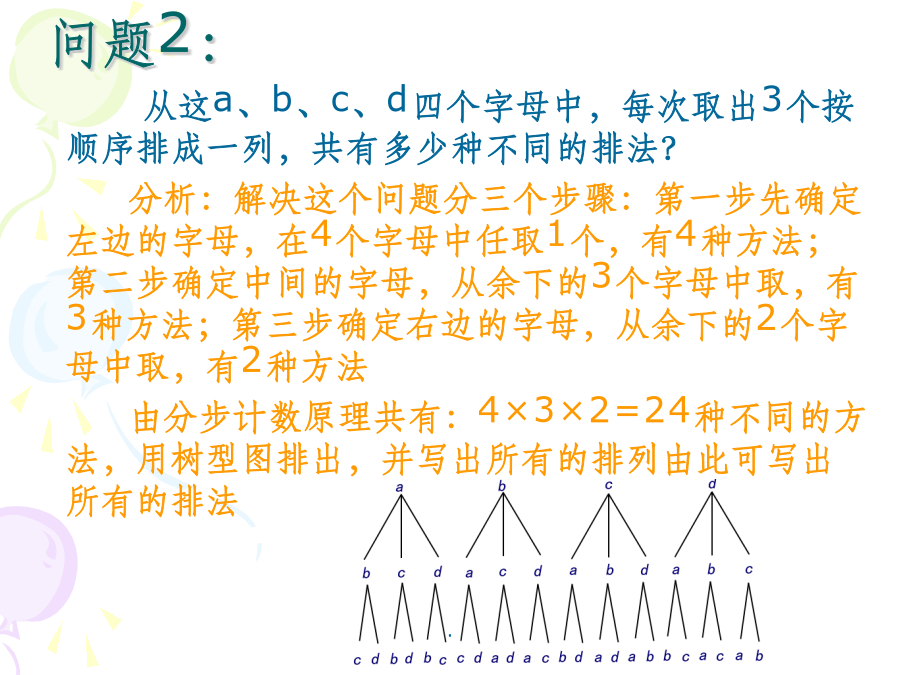
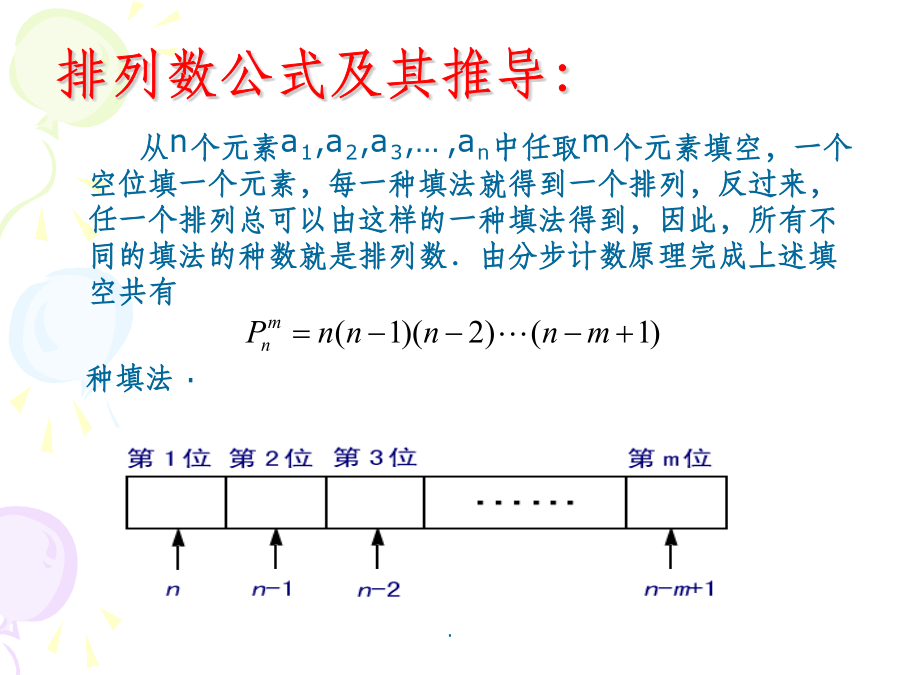
排列组合（二）——排列从甲、乙、丙3名同学中选取2名同学参加某一天的一项活动，其中一名同学参加上午的活动，一名同学参加下午的活动，有多少种不同的方法？分析：这个问题就是从甲、乙、丙3名同学中每次选取2名同学，按照参加上午的活动在前，参加下午活动在后的顺序排列，一共有多少种不同的排法的问题，共有6种不同的排法：甲乙、甲丙、乙甲、乙丙、丙甲、丙乙，其中被取的对象叫做元素问题2：排列的概念：排列数的定义：排列数公式及其推导：说明：排列数公式阶乘表示：例题：4、若，则用排列数符号表示．6、解方程（或不等式）：7、（1）从2，3，5，7，11这五个数字中，任取2个数字组成分数，不同值的分数共有多少个？（2）5人站成一排照相，共有多少种不同的站法？（3）某年全国足球中超联赛共有16队参加，每队都要与其余各队在主客场分别比赛1次，共进行多少场比赛？8、a、b、c、d、e五个人排成一排，依下列条件有多少种不同的排法？（1）共有多少种排法？（2）a必须在中间（3）a必须在两端（4）a不在首，b不在尾（5）a、b、c必须相连（6）a、b、c恰有两个相连（7）a、b、c中至多有两个相连（8）a、b、c中至少有两个相连（9）a、b、c不相连（10）a在b的前面9、用1，3，6，7，8，9组成没有重复数字且有小到大排列的四位数：（1）第114个数是多少？（2）3796是第几个数？