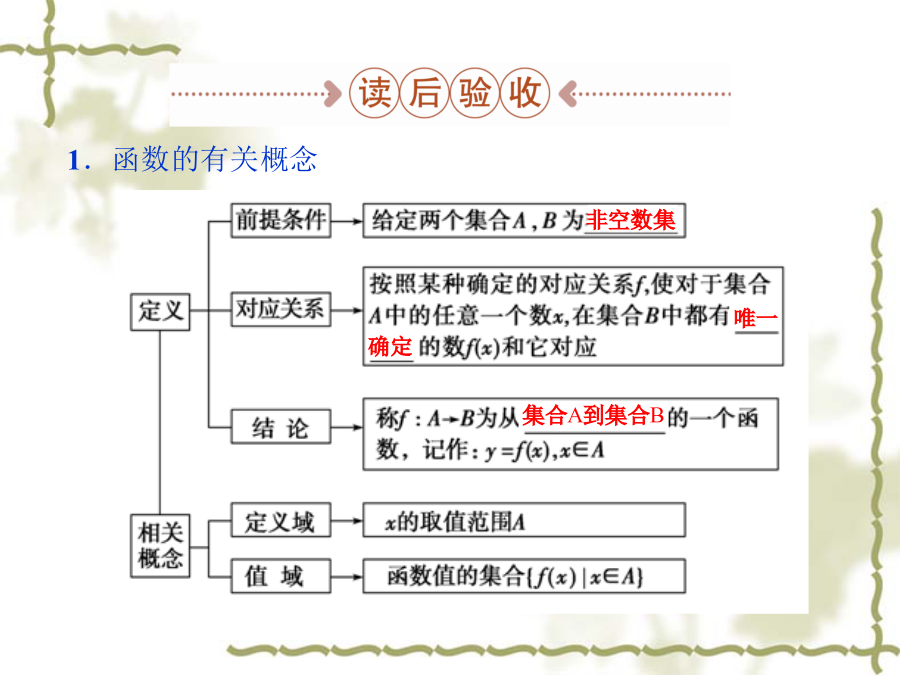
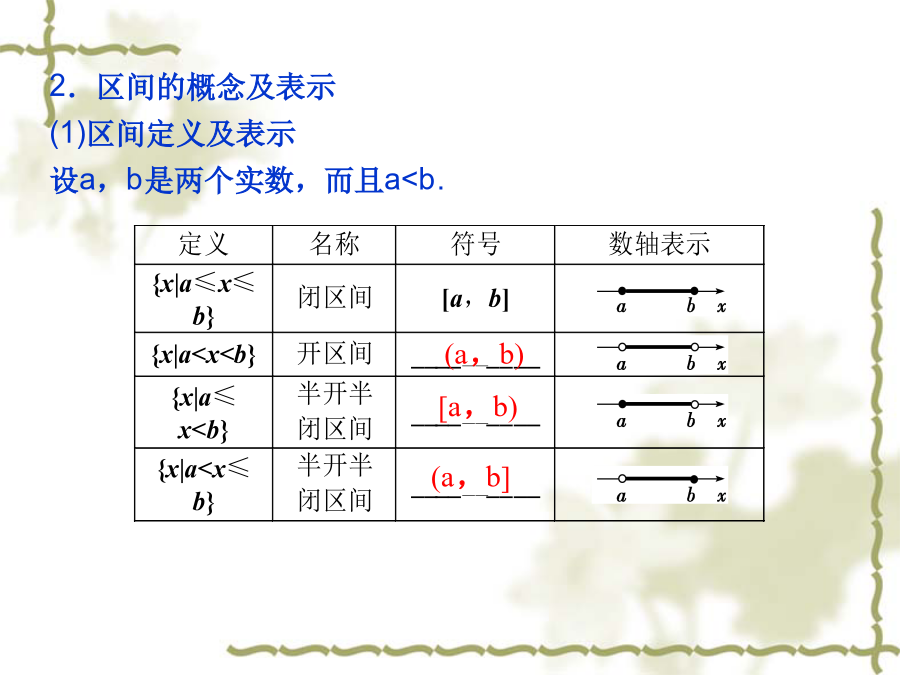
1．问题导航(1)在集合的观点下函数是怎样定义的？构成函数的要素有哪些？(2)区间是指什么样的数集？(3)相等函数是指什么样的函数？2．例题导读(1)由例1学会求函数的定义域和函数值，请试做教材P191、2题．(2)由例2学会判断两函数是否相同，进一步理解函数的基本概念，请试做教材P193题．非空数集2．区间的概念及表示(1)区间定义及表示设a，b是两个实数，而且a<b.(2)无穷概念及无穷区间表示1．判断(正确的打“√”，错误的打“×”)(1)区间表示数集，数集一定能用区间表示．()(2)数集{x|x≥2}可用区间表示为[2，＋∞]．()(3)函数的定义域和对应关系确定后，函数的值域也就确定了．()(4)函数值域中每一个数在定义域中一定只有一个数与之对应．()(5)函数的定义域和值域一定是无限集合．()D3．已知f(x)＝x2＋1，则f(2)＝________，若f(x)＝3，则x＝________．4．用区间表示下列集合：(1){x|10≤x≤100}用区间表示为________．(2){x|x>1}用区间表示为________．1．理解函数的概念应关注五点(1)“A，B是非空的数集”，一方面强调了A，B只能是数集，即A，B中的元素只能是实数；另一方面指出了定义域、值域都不能是空集，也就是说定义域为空集的函数是不存在的．(2)理解函数的概念要注意，函数的定义域是非空数集A，但函数的值域不一定是非空数集B，而是集合B的子集．(3)函数定义中强调“三性”：任意性、存在性、唯一性，即对于非空数集A中的任意一个(任意性)元素x，在非空数集B中都有(存在性)唯一(唯一性)的元素y与之对应．这三性只要有一个不满足，便不能构成函数．(4)y＝f(x)仅仅是函数符号，不是表示“y等于f与x的乘积”，f(x)也不一定就是解析式．(5)除f(x)外，有时还用g(x)、u(x)、F(x)、G(x)等符号来表示函数．2．理解区间概念的注意点(1)区间符号里面的两个字母(或数字)之间用“，”隔开；(2)区间表示实数集的几条原则：连续的数集，左端点必须小于右端点，开或闭不能混淆；(3)用数轴表示区间时，要特别注意实心点与空心点的区别；(4)由于区间是表示数集的一种形式，因此对于集合的运算仍然成立．函数的概念1．(1)下列函数与函数g(x)＝2x－1(x＞2)相等的是()A．f(m)＝2m－1(m＞2)B．f(x)＝2x－1(x∈R)C．f(x)＝2x＋1(x＞2)D．f(x)＝x－2(x＜－1)解析：对于A项，函数y＝f(m)与y＝g(x)的定义域与对应关系均相同，故为相等的函数；对于B项，两函数的定义域不同，因此不是相等的函数；对于C项，两函数的对应关系不同，因此不是相等的函数；对于D项，两函数的定义域与对应关系都不相同，故也不是相等的函数．(2)方程x2＋y＝1与x＋y2＝1是否能表示y是x(x∈R)的函数？为什么？解：x2＋y＝1能表示y是x的函数．由x2＋y＝1得y＝－x2＋1，任取一个x值都有唯一的y值和它对应．x＋y2＝1不能表示y是x的函数．取x＝0，则y＝±1；取x＝2，则没有y值和它对应．求函数的定义域求函数值和值域[互动探究]若将本例g(x)的定义域改为{0，1，2，3}，则其值域又是什么？解：因g(x)＝x2＋2，x∈{0，1，2，3}，∴g(0)＝2，g(1)＝3，g(2)＝6，g(3)＝11.∴g(x)的值域为{2，3，6，11}．方法归纳求函数值域的常用方法(1)观察法：对于一些比较简单的函数，其值域可通过观察得到；(2)配方法：此法是求“二次函数类”值域的基本方法，即把函数通过配方转化为能直接看出其值域的方法；(3)分离常数法：此方法主要是针对有理分式，即将有理分式转化为“反比例函数类”的形式，便于求值域；(4)换元法：即运用新元代换，将所给函数化成值域易确定的函数，从而求得原函数的值域．16(2)已知函数f(x)＝x2－1，求f(2x＋1)，f(x－2)．解：∵f(x)＝x2－1，∴f(2x＋1)＝(2x＋1)2－1＝4x2＋4x；f(x－2)＝(x－2)2－1＝x2－4x＋3.易错警示0≤m≤1BC能15本部分内容讲解结束